IB DP Physics: HL复习笔记9.3.5 Thin Film Interference
Thin Film Interference
- Thin film interference causes the iridescence seen in:
- Nature on peacock feathers
- Glossy flower petals
- Soap bubbles
- The shiny side of a CD
- Thin layers - or films - of oil on water
- This phenomenon occurs when light waves reflecting off the top and bottom surfaces of a thin film interfere with one another
The colourful pattern observed on a CD is a result of thin film interference
Conditions for Thin Film Interference
- To see the interference light must be incident on a material which:
- Is very thin
- Has a higher refractive index than the medium surrounding it
- Also transmits light
- The effect is caused by the reflection of waves from the top and bottom surfaces of the thin film
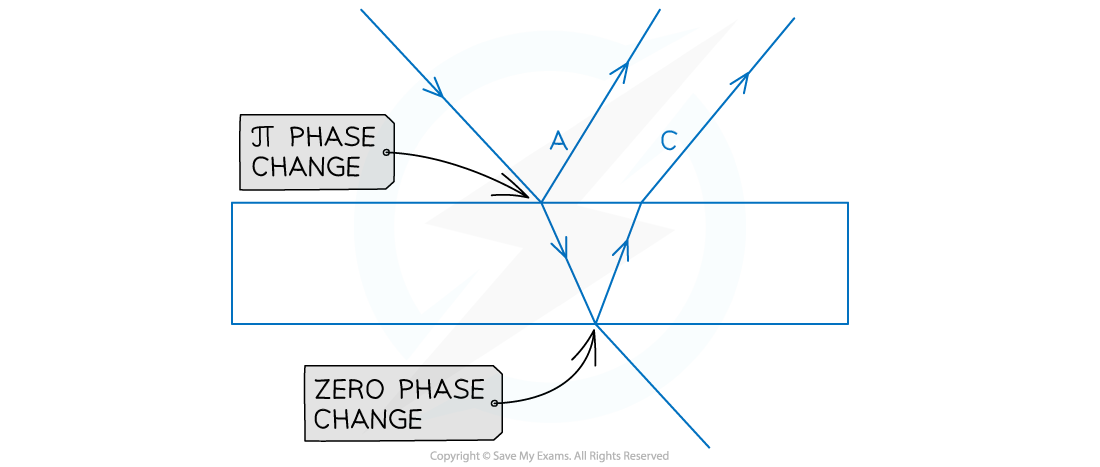
Phase changes at the top and bottom of a thin film
Light incident on the top surface of the thin film (A)
- Part of the light wave reflects at a boundary between a less-dense and a more-dense medium (e.g. Air to Oil where nair < noil ), and a phase change is seen, such that:
A wave reflected at a boundary with a medium of a higher refractive index undergoes a phase change of half a wavelength (
A wave incident on the boundary with a more dense material is both reflected and transmitted. The transmitted wave continues without a phase change and the reflected wave has a 180° phase change. What was the peak on the incident wave becomes the trough on the reflected wave.
- You need to be aware of thin-film interference for a wave incident on oil and water
- Light is reflected and transmitted from a boundary with a less dense to a more dense material
- Air to Water
- Water to Oil
- Light is reflected only from a boundary with a more dense to less dense material
- Oil to Air
- A less dense material has a lower refractive index (n)
- The refractive index of air is 1
- The refractive index of water is 1.33
- The refractive index of oil is 1.4-1.5
- Normally in thin-film interference situations: nair < noil < nwater
Light is reflected and transmitted at the boundary from a less dense to a more dense material. Light is transmitted only at the boundary from a more dense to a less dense material.
Light transmitting through the thin film (B)
- Part of the light wave also refracts as it enters the thin film and is transmitted through the material to the bottom surface
- The light wave is now travelling through a denser medium, so it travels at a slower speed and has a shorter wavelength
When the light ray enters a denser medium the wavelength becomes shorter.
Light incident on the bottom surface of the thin film (C)
- If the bottom surface is at a boundary with a more dense material (a higher refractive index e.g. oil-water where noil < nwater) then both of the following will occur:
- Reflection with a π phase change back into the thin film
- Refraction of the transmitted light into the next medium
- This is the same situation as the light wave incident on the top surface of thin film
- This is the same situation as the light wave incident on the top surface of thin film
Light is reflected only at the boundary from a more dense to a less dense material
- If the bottom surface is at a boundary with a less dense material (a lower refractive index e.g. oil-air where nair < noil ) then the following will occur:
- Reflection with no phase change back into the thin film
- No transmission or refraction will occur through the boundary
Light is transmitted with no phase change between the boundary of a less dense to a more dense material and reflected with a phase change.
Light transmitting through the thin film and refracting back into the first medium (D)
- Light travelling through the thin film undergoes a wavelength shift due to the density of the plastic
- The wavelength shift is a multiple (normally labelled m) of a half-integer multiple of wavelengths
- The thinner the film, the smaller the value of m
Light reflecting off the thin-film air boundary undergoes a wavelength shift related to the density of the thin-film. Light reflecting off the air-thin film boundary undergoes a phase change of half a wavelength. This results in constructive interference and a bright light seen by the observer.
Observing Constructive Interference
- Constructive interference will be seen as brighter colours by the observer
- The light intensity has increased making the colour appear brighter
- The total path difference of the two waves reflected and refracted off the top surface of the thin film must be a multiple of wavelengths for constructive interference to be seen by the observer
The combination of the phase change due to the reflection off the air-film surface and the phase change within the film here, results in constructive interference seen by an observer because the path difference is a multiple number of wavelengths.
- According to the data booklet, the formula for the path difference for destructive interference is:
Observing Destructive Interference
- Darker colours are observed through destructive interference
- The light intensity has decreased making the colour appear darker
- The total path difference of the two waves reflected and refracted off the top surface of the thin film must be a half-integer multiple of wavelengths for destructive interference to be seen by the observer
The combination of the phase change due to the reflection off the air-film surface and the phase change within the film here, results in destructive interference seen by an observer because the path difference is a half integer multiple number of wavelengths.
- According to the data booklet, the formula for the path difference for destructive interference is:
2dn = mλ
- Where:
- d = thickness of the film
- n = refractive index of medium
- m = an integer related to the refractive index and thickness of the medium
- λ = wavelength of the light in air
Distance Travelled inside the film
- Light travels the same distance within a thin film whether it undergoes constructive or destructive interference
- Light enters from the top surface of the thin film, passes through the thin film of thickness d
- Light is then reflected off the bottom surface travelling a further distance of d to the original surface
- So, the total distance travelled whether the light interferes constructively or destructively is 2d
The reflected wave travels a total distance of twice the thickness of the film
Model the thin film as a parallel-sided, rectangular ‘slice’ with a thickness of ‘d’
Uses of Thin Film Interference
- Thin films can prevent light from being reflected
- Due to the conservation of energy, this increases the light which is transmitted through a medium
- This effect is utilised in:
- Camera lenses - these often have a coating to prevent reflection
- Solar cells - this is to ensure a high proportion of incident light can be captured
Solving Problems Using Thin Films
The Mathematics of Constructive and Destructive Interference
- Consider a thin film, such as a soap bubble, modelled as a very thin, parallel-sided rectangle, with thickness d and refractive index higher than that of the surrounding air, i.e. n > 1
- If the thin film is sitting on top of a different denser medium e.g. water then the following situations will not apply because of the phase change obtained from the reflection at the oil-water boundary
A thin film can be modelled as a parallel-sided, rectangular ‘slice’ with a thickness of ‘d’
- Constructive interference occurs when:
Worked Example
A camera lens has a reflective coating applied to ensure that as much of the light falling on the lens is transmitted, with minimal reflection.
The lens has refractive index of 1.72 and the coating a refractive index of 1.31.
Estimate the thickness of coating required to minimise reflection of visible light. You can assume an average wavelength of 540 nm.
转载自svemyexams
翰林AMC8视频课重磅上线！
国际竞赛真题资源免费领取
