- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
1991AIME 真题及答案解析
1991AIME 真题及答案解析
答案解析请参考文末
Problem 1
Find ![]() if
if ![]() and
and ![]() are positive integers such that
are positive integers such that
Problem 2
Rectangle ![]() has sides
has sides ![]() of length 4 and
of length 4 and ![]() of length 3. Divide
of length 3. Divide ![]() into 168 congruent segments with points
into 168 congruent segments with points ![]() , and divide
, and divide ![]() into 168 congruent segments with points
into 168 congruent segments with points ![]() . For
. For ![]() , draw the segments
, draw the segments ![]() . Repeat this construction on the sides
. Repeat this construction on the sides ![]() and
and ![]() , and then draw the diagonal
, and then draw the diagonal ![]() . Find the sum of the lengths of the 335 parallel segments drawn.
. Find the sum of the lengths of the 335 parallel segments drawn.
Problem 3
Expanding ![]() by the binomial theorem and doing no further manipulation gives
by the binomial theorem and doing no further manipulation gives

 for
for Problem 4
How many real numbers ![]() satisfy the equation
satisfy the equation ![]() ?
?
Problem 5
Given a rational number, write it as a fraction in lowest terms and calculate the product of the resulting numerator and denominator. For how many rational numbers between 0 and 1 will ![]() be the resulting product?
be the resulting product?
Problem 6
Suppose ![]() is a real number for which
is a real number for which
Problem 7
Find ![]() , where
, where ![]() is the sum of the absolute values of all roots of the following equation:
is the sum of the absolute values of all roots of the following equation:

Problem 8
For how many real numbers ![]() does the quadratic equation
does the quadratic equation ![]() have only integer roots for
have only integer roots for ![]() ?
?
Problem 9
Suppose that ![]() and that
and that ![]() where
where ![]() is in lowest terms. Find
is in lowest terms. Find ![]()
Problem 10
Two three-letter strings, ![]() and
and ![]() , are transmitted electronically. Each string is sent letter by letter. Due to faulty equipment, each of the six letters has a 1/3 chance of being received incorrectly, as an
, are transmitted electronically. Each string is sent letter by letter. Due to faulty equipment, each of the six letters has a 1/3 chance of being received incorrectly, as an ![]() when it should have been a
when it should have been a ![]() , or as a
, or as a ![]() when it should be an
when it should be an ![]() . However, whether a given letter is received correctly or incorrectly is independent of the reception of any other letter. Let
. However, whether a given letter is received correctly or incorrectly is independent of the reception of any other letter. Let ![]() be the three-letter string received when
be the three-letter string received when ![]() is transmitted and let
is transmitted and let ![]() be the three-letter string received when
be the three-letter string received when ![]() is transmitted. Let
is transmitted. Let ![]() be the probability that
be the probability that ![]() comes before
comes before ![]() in alphabetical order. When
in alphabetical order. When ![]() is written as a fraction in lowest terms, what is its numerator?
is written as a fraction in lowest terms, what is its numerator?
Problem 11
Twelve congruent disks are placed on a circle ![]() of radius 1 in such a way that the twelve disks cover
of radius 1 in such a way that the twelve disks cover ![]() , no two of the disks overlap, and so that each of the twelve disks is tangent to its two neighbors. The resulting arrangement of disks is shown in the figure below. The sum of the areas of the twelve disks can be written in the form
, no two of the disks overlap, and so that each of the twelve disks is tangent to its two neighbors. The resulting arrangement of disks is shown in the figure below. The sum of the areas of the twelve disks can be written in the form ![]() , where
, where ![]() are positive integers and
are positive integers and ![]() is not divisible by the square of any prime. Find
is not divisible by the square of any prime. Find ![]() .
.
![[asy] unitsize(100); draw(Circle((0,0),1)); dot((0,0)); draw((0,0)--(1,0)); label("$1$", (0.5,0), S); for (int i=0; i<12; ++i) { dot((cos(i*pi/6), sin(i*pi/6))); } for (int a=1; a<24; a+=2) { dot(((1/cos(pi/12))*cos(a*pi/12), (1/cos(pi/12))*sin(a*pi/12))); draw(((1/cos(pi/12))*cos(a*pi/12), (1/cos(pi/12))*sin(a*pi/12))--((1/cos(pi/12))*cos((a+2)*pi/12), (1/cos(pi/12))*sin((a+2)*pi/12))); draw(Circle(((1/cos(pi/12))*cos(a*pi/12), (1/cos(pi/12))*sin(a*pi/12)), tan(pi/12))); } [/asy]](https://latex.artofproblemsolving.com/c/2/8/c28e847146e174ead38ac6c012dcb138efb2c0d0.png)
Problem 12
Rhombus ![]() is inscribed in rectangle
is inscribed in rectangle ![]() so that vertices
so that vertices ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are interior points on sides
are interior points on sides ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , respectively. It is given that
, respectively. It is given that ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Let
. Let ![]() , in lowest terms, denote the perimeter of
, in lowest terms, denote the perimeter of ![]() . Find
. Find ![]() .
.
Problem 13
A drawer contains a mixture of red socks and blue socks, at most 1991 in all. It so happens that, when two socks are selected randomly without replacement, there is a probability of exactly ![]() that both are red or both are blue. What is the largest possible number of red socks in the drawer that is consistent with this data?
that both are red or both are blue. What is the largest possible number of red socks in the drawer that is consistent with this data?
Problem 14
A hexagon is inscribed in a circle. Five of the sides have length 81 and the sixth, denoted by ![]() , has length 31. Find the sum of the lengths of the three diagonals that can be drawn from
, has length 31. Find the sum of the lengths of the three diagonals that can be drawn from ![]() .
.
Problem 15
For positive integer ![]() , define
, define ![]() to be the minimum value of the sum
to be the minimum value of the sum
1991AIME 详细解析
- Define
 and
and  . Then
. Then  and
and  . Solving these two equations yields a quadratic:
. Solving these two equations yields a quadratic:  , which factors to
, which factors to  . Either
. Either  and
and  or
or  and
and  . For the first case, it is easy to see that
. For the first case, it is easy to see that  can be
can be  (or vice versa). In the second case, since all factors of
(or vice versa). In the second case, since all factors of  must be
must be  , no two factors of
, no two factors of  can sum greater than
can sum greater than  , and so there are no integral solutions for
, and so there are no integral solutions for  . The solution is
. The solution is  .
. ![[asy] real r = 0.35; size(220); pointpen=black;pathpen=black+linewidth(0.65);pen f = fontsize(8); pair A=(0,0),B=(4,0),C=(4,3),D=(0,3); D(A--B--C--D--cycle); pair P1=A+(r,0),P2=A+(2r,0),P3=B-(r,0),P4=B-(2r,0); pair Q1=C-(0,r),Q2=C-(0,2r),Q3=B+(0,r),Q4=B+(0,2r); D(A--C);D(P1--Q1);D(P2--Q2);D(P3--Q3);D(P4--Q4); MP("A",A,f);MP("B",B,SE,f);MP("C",C,NE,f);MP("D",D,W,f); MP("P_1",P1,f);MP("P_2",P2,f);MP("P_{167}",P3,f);MP("P_{166}",P4,f);MP("Q_1",Q1,E,f);MP("Q_2",Q2,E,f);MP("Q_{167}",Q3,E,f);MP("Q_{166}",Q4,E,f); MP("4",(A+B)/2,N,f);MP("cdots",(A+B)/2,f); MP("3",(B+C)/2,W,f);MP("vdots",(C+B)/2,E,f); [/asy]](https://latex.artofproblemsolving.com/5/5/7/5578d04cdc2b7f7fa139b6bb512b5125dd621ed5.png)
 (a 3-4-5 right triangle). For each
(a 3-4-5 right triangle). For each  ,
,  is the hypotenuse of a
is the hypotenuse of a  right triangle with sides of
right triangle with sides of  . Thus, its length is
. Thus, its length is  . Let
. Let  . We want to find
. We want to find  since we are over counting the diagonal.
since we are over counting the diagonal. 
- Let
 . Then we may write
. Then we may write  . Taking logarithms in both sides of this last equation and using the well-known fact
. Taking logarithms in both sides of this last equation and using the well-known fact  (valid if
(valid if  ), we have
), we have![$log(A_{k})=logleft[frac{(N-k+1)!}{k!}x^{k}right]=logleft[prod_{j=1}^{k}frac{(N-j+1)x}{j}right]=sum_{j=1}^{k}logleft[frac{(N-j+1)x}{j}right], .$](https://latex.artofproblemsolving.com/e/e/c/eec7c7a81757012b852b8be2d3e340f10f297aa1.png) Now,
Now,  keeps increasing with
keeps increasing with  as long as the arguments
as long as the arguments  in each of the
in each of the ![$logbig[;big]$](https://latex.artofproblemsolving.com/3/9/2/39208b50ee080b4ba5232ced48e9e546ad453683.png) terms (recall that
terms (recall that  if
if  ). Therefore, the integer
). Therefore, the integer  that we are looking for must satisfy
that we are looking for must satisfy  , where
, where  denotes the greatest integer less than or equal to
denotes the greatest integer less than or equal to  .In summary, substituting
.In summary, substituting  and
and  we finally find that
we finally find that  .
. 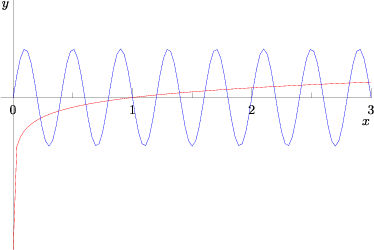
 . It is periodic (in this problem) with a period of
. It is periodic (in this problem) with a period of  .Thus,
.Thus,  , and
, and  . The solutions for
. The solutions for  occur in the domain of
occur in the domain of  . When
. When  the logarithm function returns a positive value; up to
the logarithm function returns a positive value; up to  it will pass through the sine curve. There are exactly 10 intersections of five periods (every two integral values of
it will pass through the sine curve. There are exactly 10 intersections of five periods (every two integral values of  ) of the sine curve and another curve that is
) of the sine curve and another curve that is  , so there are
, so there are  values (the subtraction of 6 since all the “intersections” when
values (the subtraction of 6 since all the “intersections” when  must be disregarded). When
must be disregarded). When  , there is exactly
, there is exactly  touching point between the two functions:
touching point between the two functions:  . When
. When  or
or  , we can count
, we can count  more solutions. The solution is
more solutions. The solution is  .
.- If the fraction is in the form
 , then
, then  and
and  . There are 8 prime numbers less than 20 (
. There are 8 prime numbers less than 20 ( ), and each can only be a factor of one of
), and each can only be a factor of one of  or
or  . There are
. There are  ways of selecting some combination of numbers for
ways of selecting some combination of numbers for  ; however, since
; however, since  , only half of them will be between
, only half of them will be between  . Therefore, the solution is
. Therefore, the solution is  .
. - There are
 numbers in the sequence. Since the terms of the sequence can be at most
numbers in the sequence. Since the terms of the sequence can be at most  apart, all of the numbers in the sequence can take one of two possible values. Since
apart, all of the numbers in the sequence can take one of two possible values. Since  , the values of each of the terms of the sequence must be either
, the values of each of the terms of the sequence must be either  or
or  . As the remainder is
. As the remainder is  ,
,  must take on
must take on  of the values, with
of the values, with  being the value of the remaining
being the value of the remaining  numbers. The 39th number is
numbers. The 39th number is  , which is also the first term of this sequence with a value of
, which is also the first term of this sequence with a value of  , so
, so  . Solving shows that
. Solving shows that  , so
, so  , and
, and  .
. - Let
 . Then
. Then  , from which we realize that
, from which we realize that  . This is because if we expand the entire expression, we will get a fraction of the form
. This is because if we expand the entire expression, we will get a fraction of the form  on the right hand side, which makes the equation simplify to a quadratic. As this quadratic will have two roots, they must be the same roots as the quadratic
on the right hand side, which makes the equation simplify to a quadratic. As this quadratic will have two roots, they must be the same roots as the quadratic  .The given finite expansion can then be easily seen to reduce to the quadratic equation
.The given finite expansion can then be easily seen to reduce to the quadratic equation  . The solutions are
. The solutions are 
 . Therefore,
. Therefore,  . We conclude that
. We conclude that  .
. - By Vieta's formulas,
 where
where  are the roots of the quadratic, and since
are the roots of the quadratic, and since  are integers,
are integers,  must be an integer. Applying the quadratic formula,
must be an integer. Applying the quadratic formula,![[x = frac{-a pm sqrt{a^2 - 24a}}{2}]](https://latex.artofproblemsolving.com/5/c/9/5c9418734aec5a2653f174c7def6c5e4f5be6df3.png) Since
Since  is an integer, we need
is an integer, we need  to be an integer (let this be
to be an integer (let this be  ):
):  . Completing the square, we get
. Completing the square, we get![[(a - 12)^2 = b^2 + 144]](https://latex.artofproblemsolving.com/b/c/6/bc6750555824e49ee620d85e9d8f542b7b1a2aa3.png) Which implies that
Which implies that  is a perfect square also (let this be
is a perfect square also (let this be  ). Then
). Then
![[c^2 - b^2 = 144 Longrightarrow (c+b)(c-b) = 144]](https://latex.artofproblemsolving.com/f/e/f/fef068ebf7b69ec2435c17b7aaaf38f76b1e3317.png)
The pairs of factors of
 are
are  ; since
; since  is the average of each respective pair and is also an integer, the pairs that work must have the same parity. Thus we get
is the average of each respective pair and is also an integer, the pairs that work must have the same parity. Thus we get  pairs (counting positive and negative) of factors that work, and substituting them backwards show that they all work.
pairs (counting positive and negative) of factors that work, and substituting them backwards show that they all work. - Use the two trigonometric Pythagorean identities
 and
and  .If we square the given
.If we square the given  , we find that
, we find that This yields
This yields  .Let
.Let  . Then squaring,
. Then squaring,
![[csc^2 x = (y - cot x)^2 Longrightarrow 1 = y^2 - 2ycot x.]](https://latex.artofproblemsolving.com/1/6/c/16ca781074f142e478d3ca701bf7599dedef1e73.png)
Substituting
 yields a quadratic equation:
yields a quadratic equation:  . It turns out that only the positive root will work, so the value of
. It turns out that only the positive root will work, so the value of  and
and  .
.Note: The problem is much easier computed if we consider what sec x is, then find the relationship between sin x and cos x (using tan x =
 , and then computing csc x + cot x using 1/sin x and then the reciprocal of tan x.
, and then computing csc x + cot x using 1/sin x and then the reciprocal of tan x. - Let us make a chart of values in alphabetical order, where
 are the probabilities that each string comes from
are the probabilities that each string comes from  and
and  multiplied by
multiplied by  , and
, and  denotes the partial sums of
denotes the partial sums of  (in other words,
(in other words,  ):
):![[begin{array}{|r||r|r|r|} hline text{String}&P_a&P_b&S_b\ hline aaa & 8 & 1 & 1 \ aab & 4 & 2 & 3 \ aba & 4 & 2 & 5 \ abb & 2 & 4 & 9 \ baa & 4 & 2 & 11 \ bab & 2 & 4 & 15 \ bba & 2 & 4 & 19 \ bbb & 1 & 8 & 27 \ hline end{array}]](https://latex.artofproblemsolving.com/4/5/a/45adb6b1a8d9c851a2622700a7be64be592dbec3.png) The probability is
The probability is  , so the answer turns out to be
, so the answer turns out to be  , and the solution is
, and the solution is  .
. - We wish to find the radius of one circle, so that we can find the total area.Notice that for them to contain the entire circle, each pair of circles must be tangent on the larger circle. Now consider two adjacent smaller circles. This means that the line connecting the radii is a segment of length
 that is tangent to the larger circle at the midpoint of the two centers. Thus, we have essentially have a regular dodecagon whose vertices are the centers of the smaller triangles circumscribed about a circle of radius
that is tangent to the larger circle at the midpoint of the two centers. Thus, we have essentially have a regular dodecagon whose vertices are the centers of the smaller triangles circumscribed about a circle of radius  .We thus know that the apothem of the dodecagon is equal to
.We thus know that the apothem of the dodecagon is equal to  . To find the side length, we make a triangle consisting of a vertex, the midpoint of a side, and the center of the dodecagon, which we denote
. To find the side length, we make a triangle consisting of a vertex, the midpoint of a side, and the center of the dodecagon, which we denote  and
and  respectively. Notice that
respectively. Notice that  , and that
, and that  is a right triangle with hypotenuse
is a right triangle with hypotenuse  and
and  . Thus
. Thus  , which is the radius of one of the circles. The area of one circle is thus
, which is the radius of one of the circles. The area of one circle is thus  , so the area of all
, so the area of all  circles is
circles is  , giving an answer of
, giving an answer of  .
.
Note that it is very useful to understand the side lengths of a 15-75-90 triangle, as these triangles often appear on higher level math contests. The side lengths are in the ratio ,
,  , and
, and 
- Let
 be the center of the rhombus. Via parallel sides and alternate interior angles, we see that the opposite triangles are congruent (
be the center of the rhombus. Via parallel sides and alternate interior angles, we see that the opposite triangles are congruent ( ,
,  ). Quickly we realize that
). Quickly we realize that  is also the center of the rectangle.By the Pythagorean Theorem, we can solve for a side of the rhombus;
is also the center of the rectangle.By the Pythagorean Theorem, we can solve for a side of the rhombus;  . Since the diagonals of a rhombus are perpendicular bisectors, we have that
. Since the diagonals of a rhombus are perpendicular bisectors, we have that  . Also,
. Also,  , so quadrilateral
, so quadrilateral  is cyclic. By Ptolemy's Theorem,
is cyclic. By Ptolemy's Theorem,  .By similar logic, we have
.By similar logic, we have  is a cyclic quadrilateral. Let
is a cyclic quadrilateral. Let  ,
,  . The Pythagorean Theorem gives us
. The Pythagorean Theorem gives us  . Ptolemy’s Theorem gives us
. Ptolemy’s Theorem gives us  . Since the diagonals of a rectangle are equal,
. Since the diagonals of a rectangle are equal,  , and
, and  . Solving for
. Solving for  , we get
, we get  . Substituting into
. Substituting into  ,
, We reject
We reject  because then everything degenerates into squares, but the condition that
because then everything degenerates into squares, but the condition that  gives us a contradiction. Thus
gives us a contradiction. Thus  , and backwards solving gives
, and backwards solving gives  . The perimeter of
. The perimeter of  is
is  , and
, and  .
. - Let
 and
and  denote the number of red and blue socks, respectively. Also, let
denote the number of red and blue socks, respectively. Also, let  . The probability
. The probability  that when two socks are drawn randomly, without replacement, both are red or both are blue is given by
that when two socks are drawn randomly, without replacement, both are red or both are blue is given by![[frac{r(r-1)}{(r+b)(r+b-1)}+frac{b(b-1)}{(r+b)(r+b-1)}=frac{r(r-1)+(t-r)(t-r-1)}{t(t-1)}=frac{1}{2}.]](https://latex.artofproblemsolving.com/6/a/5/6a5ee635ac4ad7877b78b21bc370153a2a5c9997.png) Solving the resulting quadratic equation
Solving the resulting quadratic equation  , for
, for  in terms of
in terms of  , one obtains that
, one obtains that![[r=frac{tpmsqrt{t}}{2}, .]](https://latex.artofproblemsolving.com/1/f/9/1f95ef456b38d442ab2c0165c69dd8afdda8df45.png) Now, since
Now, since  and
and  are positive integers, it must be the case that
are positive integers, it must be the case that  , with
, with  . Hence,
. Hence,  would correspond to the general solution. For the present case
would correspond to the general solution. For the present case  , and so one easily finds that
, and so one easily finds that  is the largest possible integer satisfying the problem conditions.
is the largest possible integer satisfying the problem conditions.
In summary, the solution is that the maximum number of red socks is
 .
. ![[asy]defaultpen(fontsize(9)); pair A=expi(-pi/2-acos(475/486)), B=expi(-pi/2+acos(475/486)), C=expi(-pi/2+acos(475/486)+acos(7/18)), D=expi(-pi/2+acos(475/486)+2*acos(7/18)), E=expi(-pi/2+acos(475/486)+3*acos(7/18)), F=expi(-pi/2-acos(475/486)-acos(7/18)); draw(unitcircle);draw(A--B--C--D--E--F--A);draw(A--C..A--D..A--E); dot(A^^B^^C^^D^^E^^F); label("(A)",A,(-1,-1));label("(B)",B,(1,-1));label("(C)",C,(1,0)); label("(D)",D,(1,1));label("(E)",E,(-1,1));label("(F)",F,(-1,0)); label("31",A/2+B/2,(0.7,1));label("81",B/2+C/2,(0.45,-0.2)); label("81",C/2+D/2,(-1,-1));label("81",D/2+E/2,(0,-1)); label("81",E/2+F/2,(1,-1));label("81",F/2+A/2,(1,1)); label("(x)",A/2+C/2,(-1,1));label("(y)",A/2+D/2,(1,-1.5)); label("(z)",A/2+E/2,(1,0)); [/asy]](https://latex.artofproblemsolving.com/a/5/b/a5b56caddf0c74876a022cbb3946a4eda30b38d0.png)
 ,
,  , and
, and  .Ptolemy's Theorem on
.Ptolemy's Theorem on  gives
gives  , and Ptolemy on
, and Ptolemy on  gives
gives  . Subtracting these equations give
. Subtracting these equations give  , and from this
, and from this  . Ptolemy on
. Ptolemy on  gives
gives  , and from this
, and from this  . Finally, plugging back into the first equation gives
. Finally, plugging back into the first equation gives  , so
, so  .
.- Interpret the problem geometrically. Consider
 right triangles joined at their vertices, with bases
right triangles joined at their vertices, with bases  and heights
and heights  . The sum of their hypotenuses is the value of
. The sum of their hypotenuses is the value of  . The minimum value of
. The minimum value of  , then, is the length of the straight line connecting the bottom vertex of the first right triangle and the top vertex of the last right triangle, so
, then, is the length of the straight line connecting the bottom vertex of the first right triangle and the top vertex of the last right triangle, so![[S_n ge sqrt {left(sum_{k = 1}^n (2k - 1)right)^2 + left(sum_{k = 1}^n a_kright)^2}.]](https://latex.artofproblemsolving.com/d/c/0/dc0508e085103f86c192f6dcf98a334f927655d9.png) Since the sum of the first
Since the sum of the first  odd integers is
odd integers is  and the sum of
and the sum of  is 17, we get
is 17, we get![[S_n ge sqrt {17^2 + n^4}.]](https://latex.artofproblemsolving.com/d/b/2/db280024d88e7e9e694ba3f6403019a7943178d4.png) If this is an integer, we can write
If this is an integer, we can write  , for an integer
, for an integer  . Thus,
. Thus,  The only possible value, then, for
The only possible value, then, for  is
is  , in which case
, in which case  , and
, and  .
.
以上解析方式仅供参考
学术活动报名扫码了解!免费领取历年真题!

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









