Edexcel A Level Maths: Pure:复习笔记3.2.4 Angle in a Semicircle
Angle in a Semicircle
What is the angle in a semicircle property?
- It is always possible to draw a unique circle through the three vertices of a triangle – this is called the circumcircle of the triangle
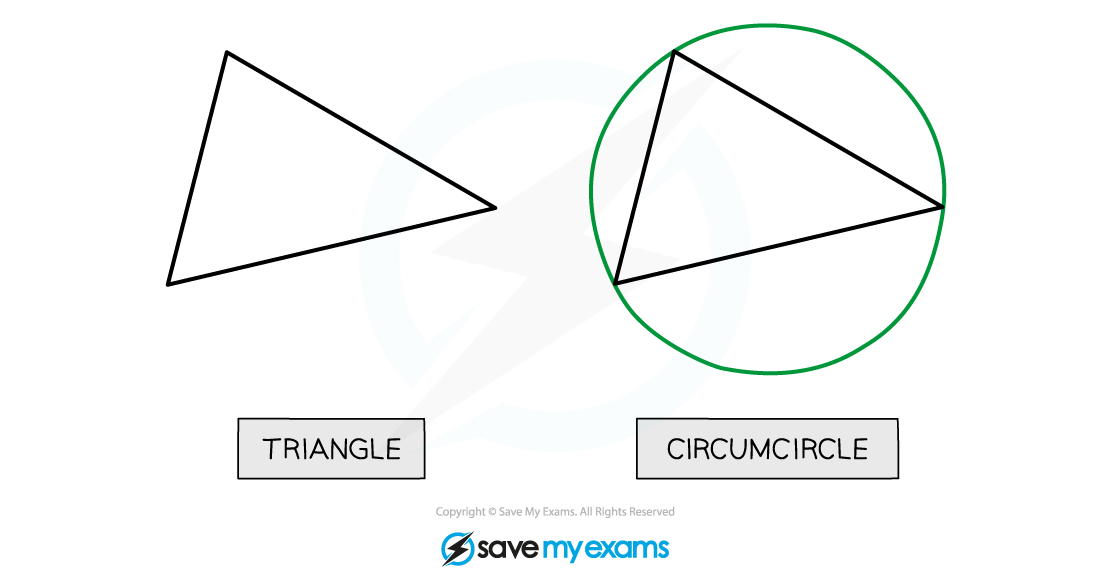
- The angle in a semicircle property says that If a triangle is right-angled, then its hypotenuse is a diameter of its circumcircle
- It also says that any angle at the circumference in a semicircle is a right angle
How can I use the angle in a semicircle property to find the equation of a circle?
- Because the hypotenuse of a right-angled triangle is a diameter of the triangle's circumcircle you also know that:
- the radius of the circumcircle is half the length of the hypotenuse
- the centre of the circumcircle is the midpoint of the hypotenuse
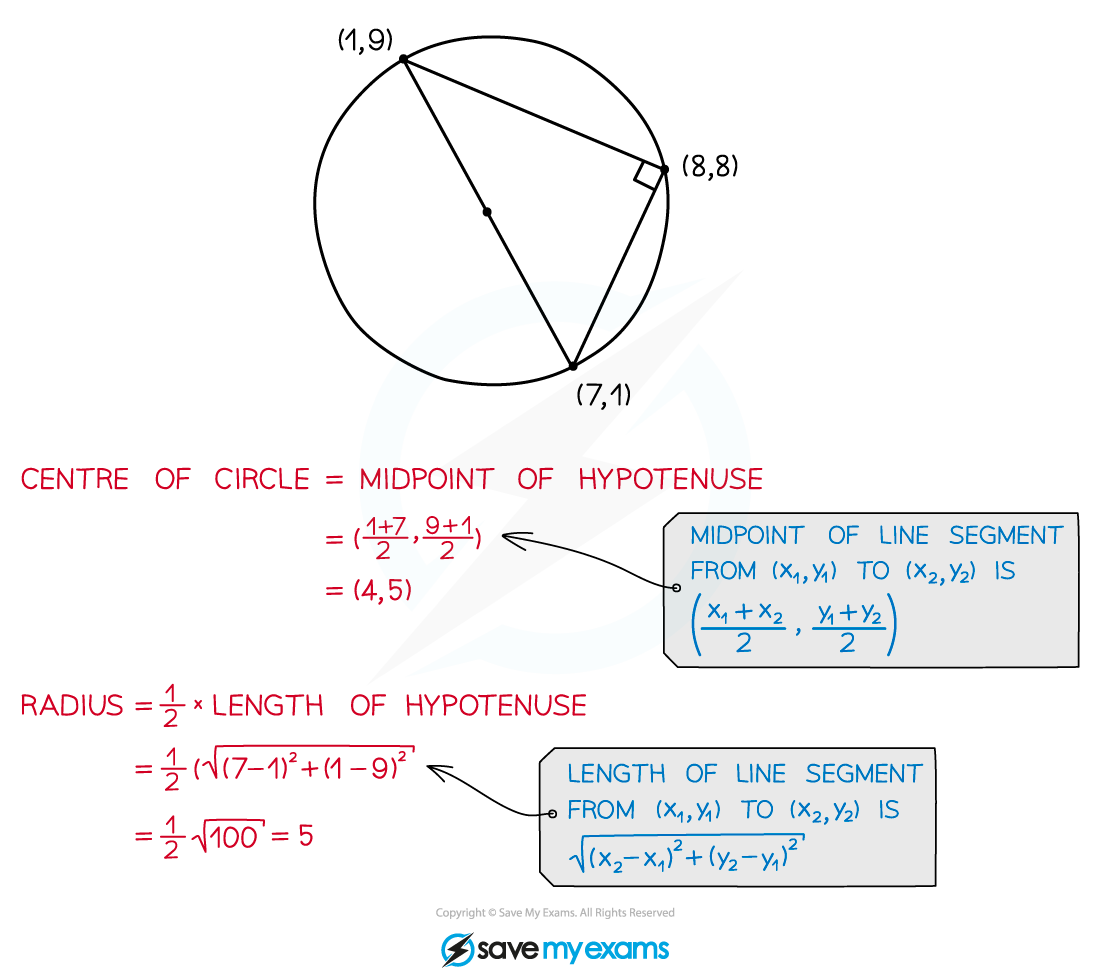
- Once you know the radius and the centre you can write down the equation of the circle
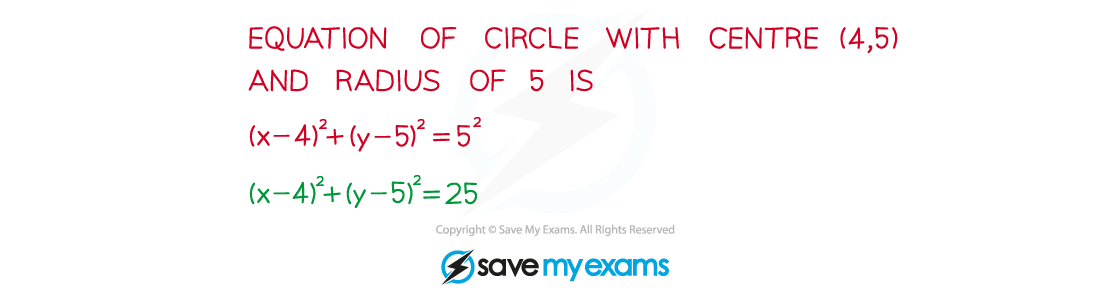
Exam Tip
- To show that a triangle is right-angled, show that the lengths of its sides satisfy Pythagoras' theorem.
Worked Example
转载自savemyexams
国际竞赛真题资料-点击免费领取！
美高学分项目重磅来袭！立即了解
