CIE A Level Maths: Pure 3复习笔记4.3.3 Parametric Equations - Sketching Graphs
Parametric Equations - Sketching Graphs
How do I sketch a graph from parametric equations?
- Plotting a graph is covered in Parametric Equations - Basics
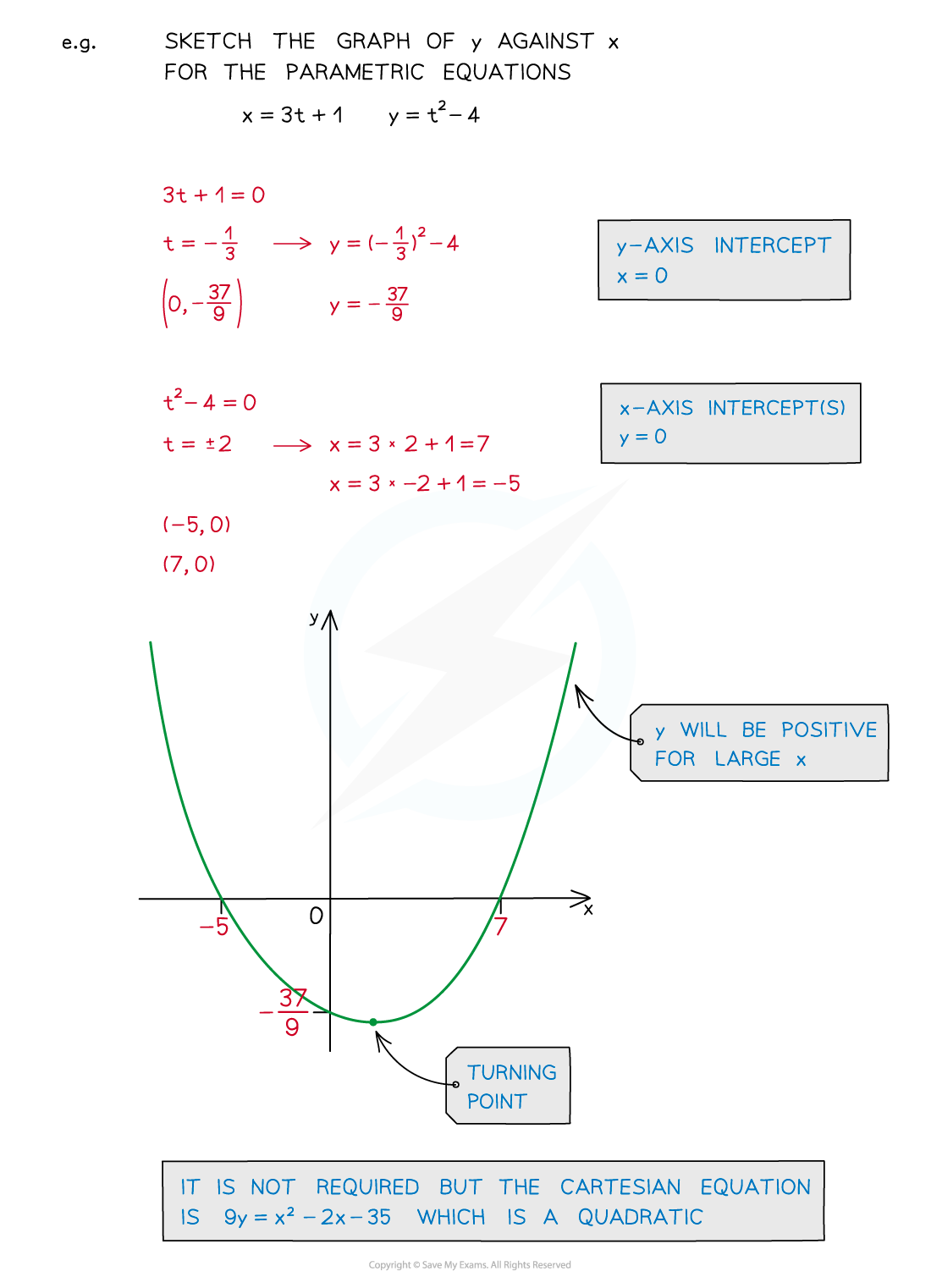
- Still find the key features of a graph …
-
- … the y-axis intercept
- … the x-axis intercept(s)
- … asymptotes
- … location of (and if required coordinates of) stationary points (see Parametric Differentiation)
- Sketch these points and join up accordingly
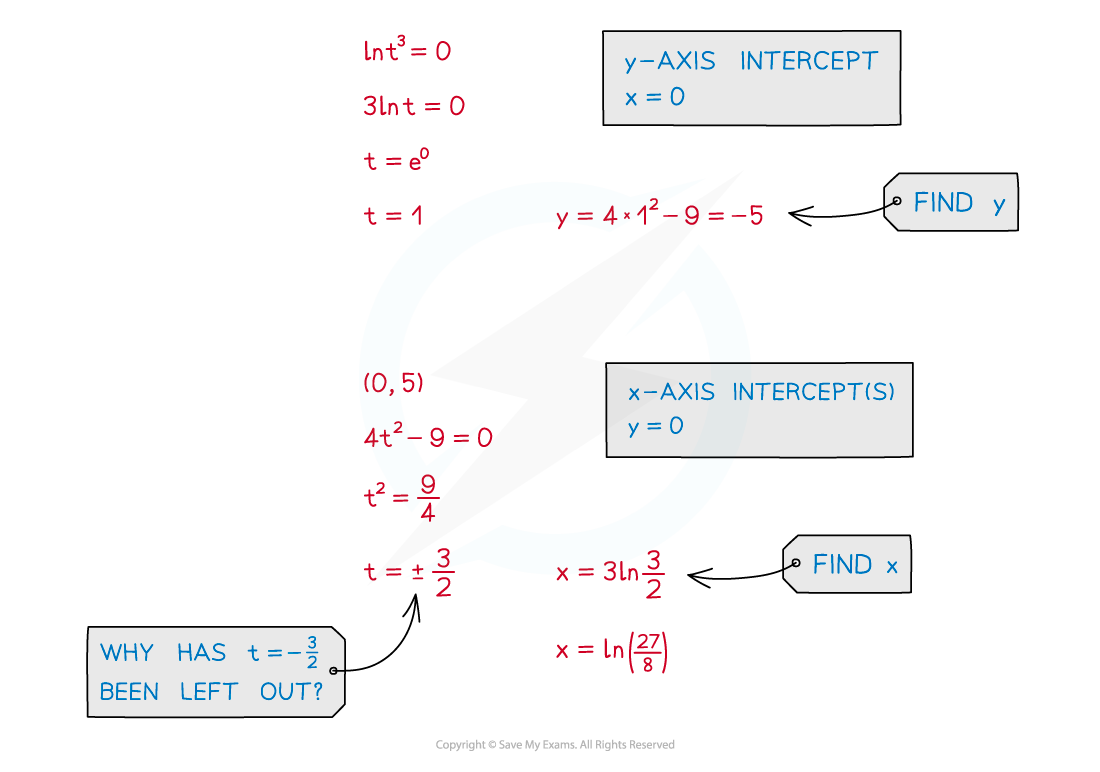
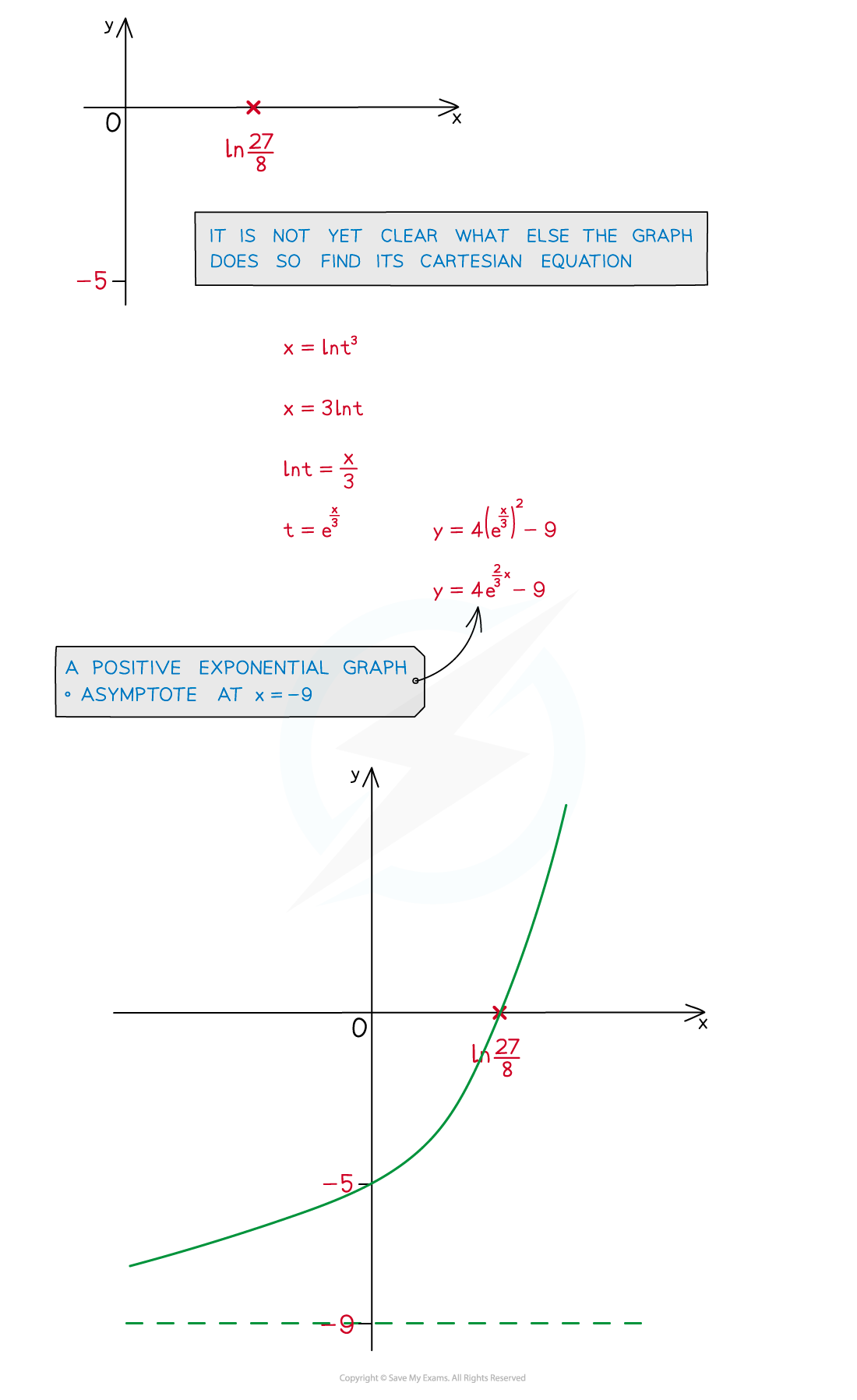
Exam Tip
- Not all curves defined parametrically lead to familiar shaped graphs and it may be worth plotting a few extra points by calculating them.
- Your calculator may be able to produce a table of values quickly, however, remember you are sketching and not plotting.
- It may be easier to find the Cartesian equation first and draw the graph from that – this will depend on the question.
- It is only a definite strategy if you cannot make progress otherwise.
- If you are given the sketch of a graph it is usually only for reference and can be used to check answers for axes intercepts, etc.
Worked Example
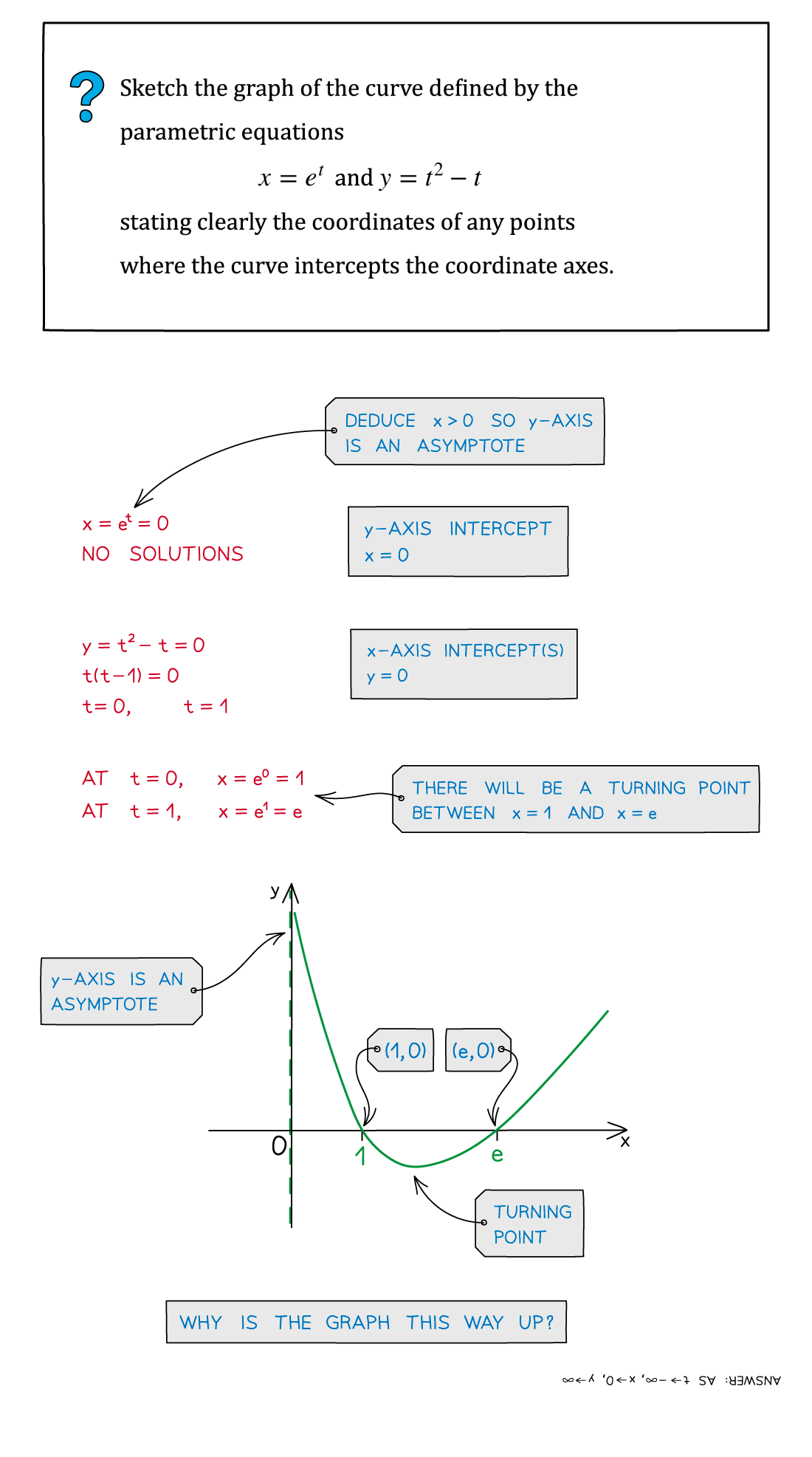
转载自savemyexams
翰林AMC8视频课重磅上线！
国际竞赛真题资源免费领取
