CIE A Level Maths: Pure 3复习笔记1.2.2 Factor & Remainder Theorem

What is the factor theorem?

• The factor theorem is a very useful result about polynomials
• A polynomial is an algebraic expression consisting of a finite number of terms, with non-negative integer indices only

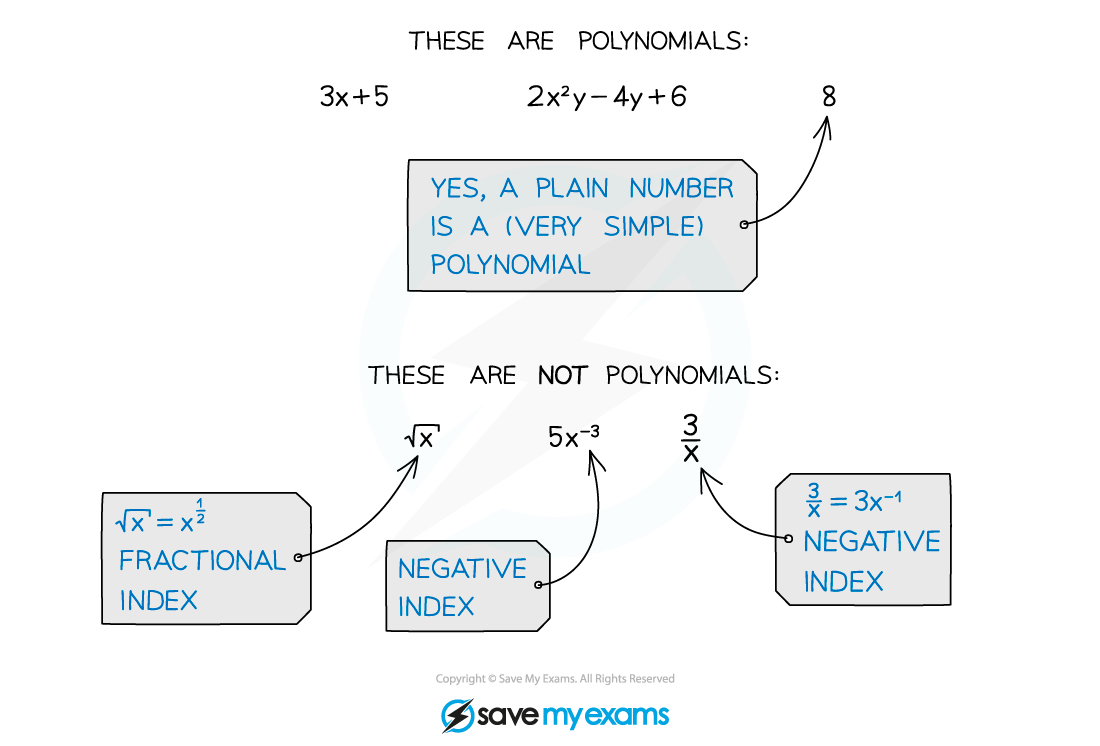
• At A level you will most frequently use the factor theorem as a way to simplify the process of factorising polynomials

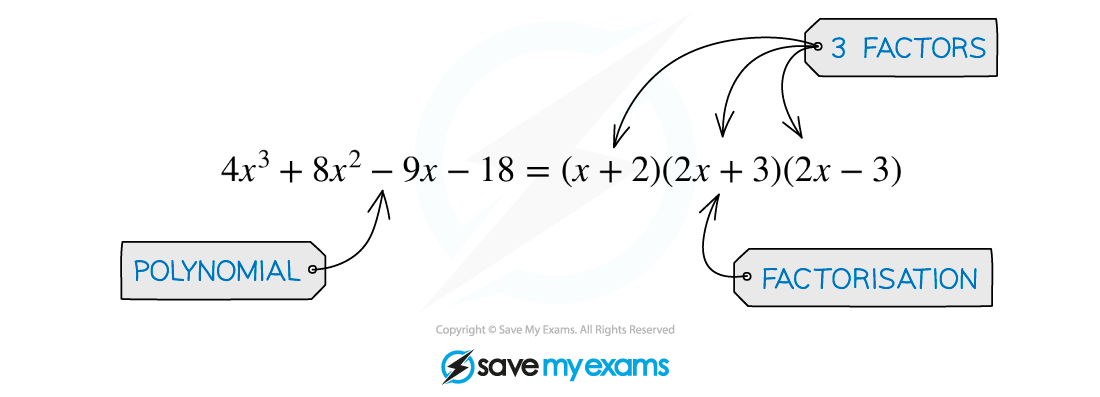
What do I need to know about the factor theorem?

• For a polynomial f(x) the factor theorem states that:
  • If f(p) = 0, then (x - p) is a factor of f(x)

  AND

• • If (x - p) is a factor of f(x), then f(p) = 0

What is the remainder theorem?

• The factor theorem is actually a special case of the more general remainder theorem
• The remainder theorem states that when the polynomial f(x) is divided by (x - a) the remainder is f(a)
  • You may see this written formally as f(x) = (x - a)Q(x) + f(a)
  • In polynomial division
    • Q(x) would be the result (at the top) of the division (the quotient)
    • f(a) would be the remainder (at the bottom)
    • (x - a) is called the divisor
  • In the case when f(a) = 0, f(x) = (x - a)Q(x) and hence (x - a) is a factor of  f(x)– the factor theorem!

How do I solve problems involving the remainder theorem?