- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2003AIME I真题及答案解析
2003AIME I真题及答案解析
答案解析请参考文末
Problem 1
Given that
Problem 2
One hundred concentric circles with radii ![]() are drawn in a plane. The interior of the circle of radius 1 is colored red, and each region bounded by consecutive circles is colored either red or green, with no two adjacent regions the same color. The ratio of the total area of the green regions to the area of the circle of radius 100 can be expressed as
are drawn in a plane. The interior of the circle of radius 1 is colored red, and each region bounded by consecutive circles is colored either red or green, with no two adjacent regions the same color. The ratio of the total area of the green regions to the area of the circle of radius 100 can be expressed as ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
Problem 3
Let the set ![]() Susan makes a list as follows: for each two-element subset of
Susan makes a list as follows: for each two-element subset of ![]() she writes on her list the greater of the set's two elements. Find the sum of the numbers on the list.
she writes on her list the greater of the set's two elements. Find the sum of the numbers on the list.
Problem 4
Given that ![]() and that
and that ![]() find
find ![]()
Problem 5
Consider the set of points that are inside or within one unit of a rectangular parallelepiped (box) that measures 3 by 4 by 5 units. Given that the volume of this set is ![]() where
where ![]() and
and ![]() are positive integers, and
are positive integers, and ![]() and
and ![]() are relatively prime, find
are relatively prime, find ![]()
Problem 6
The sum of the areas of all triangles whose vertices are also vertices of a 1 by 1 by 1 cube is ![]() where
where ![]() and
and ![]() are integers. Find
are integers. Find ![]()
Problem 7
Point ![]() is on
is on ![]() with
with ![]() and
and ![]() Point
Point ![]() is not on
is not on ![]() so that
so that ![]() and
and ![]() and
and ![]() are integers. Let
are integers. Let ![]() be the sum of all possible perimeters of
be the sum of all possible perimeters of ![]() Find
Find ![]()
Problem 8
In an increasing sequence of four positive integers, the first three terms form an arithmetic progression, the last three terms form a geometric progression, and the first and fourth terms differ by ![]() Find the sum of the four terms.
Find the sum of the four terms.
Problem 9
An integer between ![]() and
and ![]() inclusive, is called balanced if the sum of its two leftmost digits equals the sum of its two rightmost digits. How many balanced integers are there?
inclusive, is called balanced if the sum of its two leftmost digits equals the sum of its two rightmost digits. How many balanced integers are there?
Problem 10
Triangle ![]() is isosceles with
is isosceles with ![]() and
and ![]() Point
Point ![]() is in the interior of the triangle so that
is in the interior of the triangle so that ![]() and
and ![]() Find the number of degrees in
Find the number of degrees in ![]()
Problem 11
An angle ![]() is chosen at random from the interval
is chosen at random from the interval ![]() Let
Let ![]() be the probability that the numbers
be the probability that the numbers ![]() and
and ![]() are not the lengths of the sides of a triangle. Given that
are not the lengths of the sides of a triangle. Given that ![]() where
where ![]() is the number of degrees in
is the number of degrees in ![]() and
and ![]() and
and ![]() are positive integers with
are positive integers with ![]() find
find ![]()
Problem 12
In convex quadrilateral ![]() and
and ![]() The perimeter of
The perimeter of ![]() is 640. Find
is 640. Find ![]() (The notation
(The notation ![]() means the greatest integer that is less than or equal to
means the greatest integer that is less than or equal to ![]() )
)
Problem 13
Let ![]() be the number of positive integers that are less than or equal to 2003 and whose base-2 representation has more 1's than 0's. Find the remainder when
be the number of positive integers that are less than or equal to 2003 and whose base-2 representation has more 1's than 0's. Find the remainder when ![]() is divided by 1000.
is divided by 1000.
Problem 14
The decimal representation of ![]() where
where ![]() and
and ![]() are relatively prime positive integers and
are relatively prime positive integers and ![]() contains the digits 2, 5, and 1 consecutively, and in that order. Find the smallest value of
contains the digits 2, 5, and 1 consecutively, and in that order. Find the smallest value of ![]() for which this is possible.
for which this is possible.
Problem 15
In ![]() and
and ![]() Let
Let ![]() be the midpoint of
be the midpoint of ![]() and let
and let ![]() be the point on
be the point on ![]() such that
such that ![]() bisects angle
bisects angle ![]() Let
Let ![]() be the point on
be the point on ![]() such that
such that ![]() Suppose that
Suppose that ![]() meets
meets ![]() at
at ![]() The ratio
The ratio ![]() can be written in the form
can be written in the form ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
2003AIME I详细解析
- We use the definition of a factorial to get

 any larger if
any larger if  is going to stay an integer, so the answer is
is going to stay an integer, so the answer is  .
. - To get the green area, we can color all the circles of radius
 or below green, then color all those with radius
or below green, then color all those with radius  or below red, then color all those with radius
or below red, then color all those with radius  or below green, and so forth. This amounts to adding the area of the circle of radius
or below green, and so forth. This amounts to adding the area of the circle of radius  , but subtracting the circle of radius
, but subtracting the circle of radius  , then adding the circle of radius
, then adding the circle of radius  , and so forth.The total green area is thus given by
, and so forth.The total green area is thus given by  , while the total area is given by
, while the total area is given by  , so the ratio is
, so the ratio is![[frac{100^{2}pi - 99^{2}pi + 98^{2}pi - ldots - 1^{2}pi}{100^{2}pi}]](https://latex.artofproblemsolving.com/9/0/c/90cce4746c5745e82f9aeecb786972617274939f.png) For any
For any  ,
,  . We can cancel the factor of pi from the numerator and denominator and simplify the ratio to
. We can cancel the factor of pi from the numerator and denominator and simplify the ratio to![[frac{(2cdot100 - 1)+(2cdot98 - 1) + ldots + (2cdot 2 - 1)}{100^{2}} = frac{2cdot(100 + 98 + ldots + 2) - 50}{100^2}.]](https://latex.artofproblemsolving.com/1/5/a/15ae4396f4310c9f044746926b12ab3d7fb0a249.png) Using the formula for the sum of an arithmetic series, we see that this is equal to
Using the formula for the sum of an arithmetic series, we see that this is equal to![[frac{2(50)(51)-50}{100^{2}}=frac{50(101)}{100^{2}}=frac{101}{200},]](https://latex.artofproblemsolving.com/c/6/5/c65689a1294918b1d1100973338c70145e034ed8.png)
so the answer is
 .
.
Alternatively, we can determine a pattern through trial-and-error using smaller numbers.
- For
 circles, the ratio is
circles, the ratio is  .
. - For
 circles, the ratio is
circles, the ratio is  .
. - For
 circles, the ratio is
circles, the ratio is  .
. - For
 circles, the ratio is
circles, the ratio is  .
.
Now the pattern for each ratio is clear. Given
 circles, the ratio is
circles, the ratio is  . For the
. For the  circle case (which is what this problem is),
circle case (which is what this problem is),  , and the ratio is
, and the ratio is  .
.
Also, using the difference of squares, the expression simplifies to
 . We can easily determine the sum with
. We can easily determine the sum with  . Simplifying gives us
. Simplifying gives us  and the answer is
and the answer is  .
. - For
- Order the numbers in the set from greatest to least to reduce error:
 Each element of the set will appear in
Each element of the set will appear in  two-element subsets, once with each other number.
two-element subsets, once with each other number.
 will be the greater number in
will be the greater number in  subsets.
subsets. will be the greater number in
will be the greater number in  subsets.
subsets. will be the greater number in
will be the greater number in  subsets.
subsets. will be the greater number in
will be the greater number in  subsets.
subsets. will be the greater number in
will be the greater number in  subsets.
subsets. will be the greater number in
will be the greater number in  subsets.
subsets. will be the greater number in
will be the greater number in  subsets.
subsets. will be the greater number in
will be the greater number in  subsets.
subsets.
Therefore the desired sum is
 .
. - Using the properties of logarithms, we can simplify the first equation to
 . Therefore,
. Therefore,![[sin x cos x = frac{1}{10}.qquad (*)]](https://latex.artofproblemsolving.com/d/c/2/dc278590c1d813f4bd28263eb411e3cf6eedfc08.png) Now, manipulate the second equation.
Now, manipulate the second equation. By the Pythagorean identities,
By the Pythagorean identities,  , and we can substitute the value for
, and we can substitute the value for  from
from  .
.  .
. - The set can be broken into several parts: the big
 parallelepiped,
parallelepiped,  external parallelepipeds that each share a face with the large parallelepiped and have a height of
external parallelepipeds that each share a face with the large parallelepiped and have a height of  , the
, the  spheres (one centered at each vertex of the large parallelepiped), and the
spheres (one centered at each vertex of the large parallelepiped), and the  cylinders connecting each adjacent pair of spheres.
cylinders connecting each adjacent pair of spheres.
- The volume of the parallelepiped is
 cubic units.
cubic units. - The volume of the external parallelepipeds is
 .
. - There are
 of the
of the  spheres, each of radius
spheres, each of radius  . Together, their volume is
. Together, their volume is  .
. - There are
 of the
of the  cylinders, so
cylinders, so  complete cylinders can be formed. Their volumes are
complete cylinders can be formed. Their volumes are  ,
,  , and
, and  , adding up to
, adding up to  .
.
The combined volume of these parts is
 . Thus, the answer is
. Thus, the answer is  .
. - The volume of the parallelepiped is
- Since there are
 vertices of a cube, there are
vertices of a cube, there are  total triangles to consider. They fall into three categories: there are those which are entirely contained within a single face of the cube (whose sides are two edges and one face diagonal), those which lie in a plane perpendicular to one face of the cube (whose sides are one edge, one face diagonal and one space diagonal of the cube) and those which lie in a plane oblique to the edges of the cube, whose sides are three face diagonals of the cube.Each face of the cube contains
total triangles to consider. They fall into three categories: there are those which are entirely contained within a single face of the cube (whose sides are two edges and one face diagonal), those which lie in a plane perpendicular to one face of the cube (whose sides are one edge, one face diagonal and one space diagonal of the cube) and those which lie in a plane oblique to the edges of the cube, whose sides are three face diagonals of the cube.Each face of the cube contains  triangles of the first type, and there are
triangles of the first type, and there are  faces, so there are
faces, so there are  triangles of the first type. Each of these is a right triangle with legs of length
triangles of the first type. Each of these is a right triangle with legs of length  , so each triangle of the first type has area
, so each triangle of the first type has area  .Each edge of the cube is a side of exactly
.Each edge of the cube is a side of exactly  of the triangles of the second type, and there are
of the triangles of the second type, and there are  edges, so there are
edges, so there are  triangles of the second type. Each of these is a right triangle with legs of length
triangles of the second type. Each of these is a right triangle with legs of length  and
and  , so each triangle of the second type has area
, so each triangle of the second type has area  .Each vertex of the cube is associated with exactly one triangle of the third type (whose vertices are its three neighbors), and there are
.Each vertex of the cube is associated with exactly one triangle of the third type (whose vertices are its three neighbors), and there are  vertices of the cube, so there are
vertices of the cube, so there are  triangles of the third type. Each of the these is an equilateral triangle with sides of length
triangles of the third type. Each of the these is an equilateral triangle with sides of length  , so each triangle of the third type has area
, so each triangle of the third type has area  .Thus the total area of all these triangles is
.Thus the total area of all these triangles is  and the answer is
and the answer is  .
. - Denote the height of
 as
as  ,
,  , and
, and  . Using the Pythagorean theorem, we find that
. Using the Pythagorean theorem, we find that  and
and  . Thus,
. Thus,  . The LHS is difference of squares, so
. The LHS is difference of squares, so  . As both
. As both  are integers,
are integers,  must be integral divisors of
must be integral divisors of  .The pairs of divisors of
.The pairs of divisors of  are
are  . This yields the four potential sets for
. This yields the four potential sets for  as
as  . The last is not a possibility since it simply degenerates into a line. The sum of the three possible perimeters of
. The last is not a possibility since it simply degenerates into a line. The sum of the three possible perimeters of  is equal to
is equal to  .Using Stewart's Theorem, letting the side length be c, and the cevian be d, then we have
.Using Stewart's Theorem, letting the side length be c, and the cevian be d, then we have  . Dividing both sides by thirty leaves
. Dividing both sides by thirty leaves  . The solution follows as above.
. The solution follows as above. - Denote the first term as
 , and the common difference between the first three terms as
, and the common difference between the first three terms as  . The four numbers thus are in the form
. The four numbers thus are in the form  .Since the first and fourth terms differ by
.Since the first and fourth terms differ by  , we have that
, we have that  . Multiplying out by the denominator,
. Multiplying out by the denominator,![[(a^2 + 4ad + 4d^2) - a(a + d) = 30(a + d).]](https://latex.artofproblemsolving.com/0/7/f/07fd58d0963b72126bae86ec79dbb742881168b1.png) This simplifies to
This simplifies to  , which upon rearranging yields
, which upon rearranging yields  .Both
.Both  and
and  are positive integers, so
are positive integers, so  and
and  must have the same sign. Try if they are both positive (notice if they are both negative, then
must have the same sign. Try if they are both positive (notice if they are both negative, then  and
and  , which is a contradiction). Then,
, which is a contradiction). Then,  . Directly substituting and testing shows that
. Directly substituting and testing shows that  , but that if
, but that if  then
then  . Alternatively, note that
. Alternatively, note that  or
or  implies that
implies that  , so only
, so only  may work. Hence, the four terms are
may work. Hence, the four terms are  , which indeed fits the given conditions. Their sum is
, which indeed fits the given conditions. Their sum is  .
. - If the common sum of the first two and last two digits is
 , such that
, such that  , there are
, there are  choices for the first two digits and
choices for the first two digits and  choices for the second two digits (since zero may not be the first digit). This gives
choices for the second two digits (since zero may not be the first digit). This gives  balanced numbers. If the common sum of the first two and last two digits is
balanced numbers. If the common sum of the first two and last two digits is  , such that
, such that  , there are
, there are  choices for both pairs. This gives
choices for both pairs. This gives  balanced numbers. Thus, there are in total
balanced numbers. Thus, there are in total  balanced numbers.Both summations may be calculated using the formula for the sum of consecutive squares, namely
balanced numbers.Both summations may be calculated using the formula for the sum of consecutive squares, namely  .
. ![[asy] pointpen = black; pathpen = black+linewidth(0.7); size(220); /* We will WLOG AB = 2 to draw following */ pair A=(0,0), B=(2,0), C=(1,Tan(37)), M=IP(A--(2Cos(30),2Sin(30)),B--B+(-2,2Tan(23))), N=(2-M.x,M.y); D(MP("A",A)--MP("B",B)--MP("C",C,N)--cycle); D(A--D(MP("M",M))--B); D(C--M); D(C--D(MP("N",N))--B--N--M,linetype("6 6")+linewidth(0.7)); [/asy]](https://latex.artofproblemsolving.com/e/c/8/ec8d127e80906c0e7baf73d163450eef066397cc.png)
 inside
inside  such that
such that  and
and  .
. . Also, since
. Also, since  and
and  are congruent (by ASA),
are congruent (by ASA),  . Hence
. Hence  is an equilateral triangle, so
is an equilateral triangle, so  .Then
.Then  . We now see that
. We now see that  and
and  are congruent. Therefore,
are congruent. Therefore,  , so
, so  .From the givens, we have the following angle measures:
.From the givens, we have the following angle measures:  ,
,  . If we define
. If we define  then we also have
then we also have  . Then apply the Law of Sines to triangles
. Then apply the Law of Sines to triangles  and
and  to get
to get![[frac{sin 150^circ}{sin 7^circ} = frac{AC}{CM} = frac{BC}{CM} = frac{sin theta}{sin (97^circ - theta)}]](https://latex.artofproblemsolving.com/0/b/a/0ba2b582bcb8aca8d0fcbca0e142e071352eb30f.png) Clearing denominators, evaluating
Clearing denominators, evaluating  and applying one of our trigonometric identities to the result gives
and applying one of our trigonometric identities to the result gives
![[frac{1}{2} cos (7^circ - theta )= sin 7^circ sin theta]](https://latex.artofproblemsolving.com/8/9/c/89c211497b262b45d3aeb2a00921f315194b202f.png)
and multiplying through by 2 and applying the double angle formulas gives
![[cos 7^circcostheta + sin7^circsintheta = 2 sin7^circ sintheta]](https://latex.artofproblemsolving.com/a/e/f/aef237179cb2c6f4f96e5c906ab00cf00cdf20a3.png)
and so
 ; since
; since  , we must have
, we must have  , so the answer is
, so the answer is  .
.- Note that the three expressions are symmetric with respect to interchanging
 and
and  , and so the probability is symmetric around
, and so the probability is symmetric around  . Thus, take
. Thus, take  so that
so that  . Then
. Then  is the largest of the three given expressions and those three lengths not forming a triangle is equivalent to a violation of the triangle inequality
is the largest of the three given expressions and those three lengths not forming a triangle is equivalent to a violation of the triangle inequality![[cos^2 x > sin^2 x + sin x cos x]](https://latex.artofproblemsolving.com/e/9/5/e9517416a3c31919329a0da7536cd7ea943ff949.png) This is equivalent to
This is equivalent to![[cos^2 x - sin^2 x > sin x cos x]](https://latex.artofproblemsolving.com/d/0/0/d00b48f38038b52b18c0bed05b4995a6adef3920.png) and, using some of our trigonometric identities, we can re-write this as
and, using some of our trigonometric identities, we can re-write this as  . Since we've chosen
. Since we've chosen  ,
,  so
so![[2 > tan 2x Longrightarrow x < frac 12 arctan 2.]](https://latex.artofproblemsolving.com/f/1/1/f1190e08567586a123631e30e1c61bdeb88563a8.png)
The probability that
 lies in this range is
lies in this range is  so that
so that  ,
,  and our answer is
and our answer is  .
. - By the Law of Cosines on
 at angle
at angle  and on
and on  at angle
at angle  (note
(note  ),
),![[180^2 + AD^2 - 360 cdot AD cos A = 180^2 + BC^2 - 360 cdot BC cos A]](https://latex.artofproblemsolving.com/0/7/e/07e1af8523ab205d2d11514700ad107115f4eea0.png)
![[(AD^2 - BC^2) = 360(AD - BC) cos A]](https://latex.artofproblemsolving.com/a/d/d/addbce636fbcd974396b348f61cf12eac185211c.png)
![[(AD - BC)(AD + BC) = 360(AD - BC) cos A]](https://latex.artofproblemsolving.com/6/6/1/661af1da247a134ac8796756aed6607b56a826aa.png)
![[(AD + BC) = 360 cos A]](https://latex.artofproblemsolving.com/b/c/3/bc31dcd0f1be036f707b187366e53ebd9b90b9cd.png) We know that
We know that  .
. 
 .Notice that
.Notice that  , and
, and  , and
, and  , so we have side-side-angle matching on triangles
, so we have side-side-angle matching on triangles  and
and  . Since the problem does not allow
. Since the problem does not allow  , we know that
, we know that  is not a right angle, and there is a unique other triangle with the matching side-side-angle.Extend
is not a right angle, and there is a unique other triangle with the matching side-side-angle.Extend  to
to  so that
so that  is isosceles with
is isosceles with  . Then notice that
. Then notice that  has matching side-side-angle, and yet
has matching side-side-angle, and yet  because
because  is not right. Therefore
is not right. Therefore  is the unique triangle mentioned above, so
is the unique triangle mentioned above, so  is congruent, in some order of vertices, to
is congruent, in some order of vertices, to  . Since
. Since  would imply
would imply  , making quadrilateral
, making quadrilateral  degenerate, we must have
degenerate, we must have  .Since the perimeter of
.Since the perimeter of  is
is  ,
,  . Hence
. Hence  . Drop the altitude of
. Drop the altitude of  from
from  and call the foot
and call the foot  . Then right triangle trigonometry on
. Then right triangle trigonometry on  shows that
shows that  , so
, so  .
. - In base-
 representation, all positive numbers have a leftmost digit of
representation, all positive numbers have a leftmost digit of  . Thus there are
. Thus there are  numbers that have
numbers that have  digits in base
digits in base  notation, with
notation, with  of the digits being
of the digits being  's.In order for there to be more
's.In order for there to be more  's than
's than  's, we must have
's, we must have  . Therefore, the number of such numbers corresponds to the sum of all numbers on or to the right of the vertical line of symmetry in Pascal's Triangle, from rows
. Therefore, the number of such numbers corresponds to the sum of all numbers on or to the right of the vertical line of symmetry in Pascal's Triangle, from rows  to
to  (as
(as  ). Since the sum of the elements of the
). Since the sum of the elements of the  th row is
th row is  , it follows that the sum of all elements in rows
, it follows that the sum of all elements in rows  through
through  is
is  . The center elements are in the form
. The center elements are in the form  , so the sum of these elements is
, so the sum of these elements is  .The sum of the elements on or to the right of the line of symmetry is thus
.The sum of the elements on or to the right of the line of symmetry is thus  . However, we also counted the
. However, we also counted the  numbers from
numbers from  to
to  . Indeed, all of these numbers have at least
. Indeed, all of these numbers have at least 
 's in their base-
's in their base- representation, as all of them are greater than
representation, as all of them are greater than  , which has
, which has 
 's. Therefore, our answer is
's. Therefore, our answer is  , and the remainder is
, and the remainder is  .We seek the number of allowed numbers which have
.We seek the number of allowed numbers which have  1's, not including the leading 1, for
1's, not including the leading 1, for  .For
.For  , this number is
, this number is .
.
By the Hockey Stick Identity, this is equal to
 . So we get
. So we get .
.For
 , we end on
, we end on  - we don't want to consider numbers with more than 11 digits. So for each
- we don't want to consider numbers with more than 11 digits. So for each  we get
we get
again by the Hockey Stick Identity. So we get
 .
.The total is
 . Subtracting out the
. Subtracting out the  numbers between
numbers between  and
and  gives
gives  . Thus the answer is
. Thus the answer is  .
. - To find the smallest value of
 , we consider when the first three digits after the decimal point are
, we consider when the first three digits after the decimal point are  .Otherwise, suppose the number is in the form of
.Otherwise, suppose the number is in the form of  , where
, where  is a string of
is a string of  digits and
digits and  is small as possible. Then
is small as possible. Then  . Since
. Since  is an integer and
is an integer and  is a fraction between
is a fraction between  and
and  , we can rewrite this as
, we can rewrite this as  , where
, where  . Then the fraction
. Then the fraction  suffices.Thus we have
suffices.Thus we have  , or
, or
 , we know that the minimum value of
, we know that the minimum value of  is
is  ; hence we need
; hence we need  . Since
. Since  , we need
, we need  to be divisible by
to be divisible by  , and this first occurs when
, and this first occurs when  (note that if
(note that if  , then
, then  ). Indeed, this gives
). Indeed, this gives  and the fraction
and the fraction  ).
). - In the following, let the name of a point represent the mass located there. Since we are looking for a ratio, we assume that
 ,
,  , and
, and  in order to simplify our computations.First, reflect point
in order to simplify our computations.First, reflect point  over angle bisector
over angle bisector  to a point
to a point  .
.![[asy] size(400); pointpen = black; pathpen = black+linewidth(0.7); pair A=(0,0),C=(7.8,0),B=IP(CR(A,3.6),CR(C,5.07)), M=(A+C)/2, Da = bisectorpoint(A,B,C), D=IP(B--B+(Da-B)*10,A--C), F=IP(D--D+10*(B-D)*dir(270),B--C), E=IP(B--M,D--F);pair Fprime=2*D-F; /* scale down by 100x */ D(MP("A",A,NW)--MP("B",B,N)--MP("C",C)--cycle); D(B--D(MP("D",D))--D(MP("F",F,NE))); D(B--D(MP("M",M)));D(A--MP("F'",Fprime,SW)--D); MP("E",E,NE); D(rightanglemark(F,D,B,4)); MP("390",(M+C)/2); MP("390",(M+C)/2); MP("360",(A+B)/2,NW); MP("507",(B+C)/2,NE); [/asy]](https://latex.artofproblemsolving.com/d/5/2/d52650d1c43c62a6df30fc3e7b09651eb4cf6b37.png)
 is an angle bisector of both triangles
is an angle bisector of both triangles  and
and  , we know that
, we know that  lies on
lies on  . We can now balance triangle
. We can now balance triangle  at point
at point  using mass points.By the Angle Bisector Theorem, we can place mass points on
using mass points.By the Angle Bisector Theorem, we can place mass points on  of
of  respectively. Thus, a mass of
respectively. Thus, a mass of  belongs at both
belongs at both  and
and  because BD is a median of triangle
because BD is a median of triangle  . Therefore,
. Therefore,  .Now, we reassign mass points to determine
.Now, we reassign mass points to determine  . This setup involves
. This setup involves  and transversal
and transversal  . For simplicity, put masses of
. For simplicity, put masses of  and
and  at
at  and
and  respectively. To find the mass we should put at
respectively. To find the mass we should put at  , we compute
, we compute  . Applying the Angle Bisector Theorem again and using the fact
. Applying the Angle Bisector Theorem again and using the fact  is a midpoint of
is a midpoint of  , we find
, we find![[frac {MD}{CM} = frac {frac{169}{289}cdot 260 - 130}{130} = frac {49}{289}]](https://latex.artofproblemsolving.com/8/9/0/89026ab2d403a93d26a9d2b32cb9887f4f166b5b.png) At this point we could find the mass at
At this point we could find the mass at  but it's unnecessary.
but it's unnecessary.![[frac {DE}{EF} = frac {F}{D} = frac {F}{C}cdotfrac {C}{D} = frac {289}{240}cdotfrac {49}{289} = boxed{frac {49}{240}}]](https://latex.artofproblemsolving.com/9/7/c/97c235f9f50f5080b9acedec60af96d75079d9e6.png) and the answer is
and the answer is  .By the Angle Bisector Theorem, we know that
.By the Angle Bisector Theorem, we know that ![$[CBD]=frac{169}{289}[ABC]$](https://latex.artofproblemsolving.com/8/7/7/8770244aa9d09e5cc835149d7d59a4f389e415a1.png) . Therefore, by finding the area of triangle
. Therefore, by finding the area of triangle  , we see that
, we see that![[frac{507cdot BD}{2}sinfrac{B}{2}=frac{169}{289}[ABC].]](https://latex.artofproblemsolving.com/c/0/6/c0650a5ecb58e33cd172fe6ef3a31d8c14ceeb8c.png) Solving for
Solving for  yields
yields![[BD=frac{2[ABC]}{3cdot289sinfrac{B}{2}}.]](https://latex.artofproblemsolving.com/a/1/0/a10b4e65dae4de953d8cd79f97c5cdd90821c226.png) Furthermore,
Furthermore,  , so
, so![[BF=frac{BD}{cosfrac{B}{2}}=frac{2[ABC]}{3cdot289sinfrac{B}{2}cosfrac{B}{2}}.]](https://latex.artofproblemsolving.com/a/1/f/a1f127e944b543d0ea9689083304c3e7b9a59367.png) Now by the identity
Now by the identity  , we get
, we get![[BF=frac{4[ABC]}{3cdot289sin B}.]](https://latex.artofproblemsolving.com/e/e/a/eea19462c9f3a077e1bac31685913789c964fded.png) But then
But then ![$[ABC]=frac{360cdot 507}{2}sin B$](https://latex.artofproblemsolving.com/5/d/c/5dce202b5ba7d0705b180c5cd96a544121765f9a.png) , so
, so  . Thus
. Thus  .
.
Now by the Angle Bisector Theorem,
 , and we know that
, and we know that  so
so  .
.We can now use mass points on triangle CBD. Assign a mass of
 to point
to point  . Then
. Then  must have mass
must have mass  and
and  must have mass
must have mass  . This gives
. This gives  a mass of
a mass of  . Therefore,
. Therefore,  , giving us an answer of
, giving us an answer of 
以上解析方式仅供参考
学术活动报名扫码了解!免费领取历年真题!
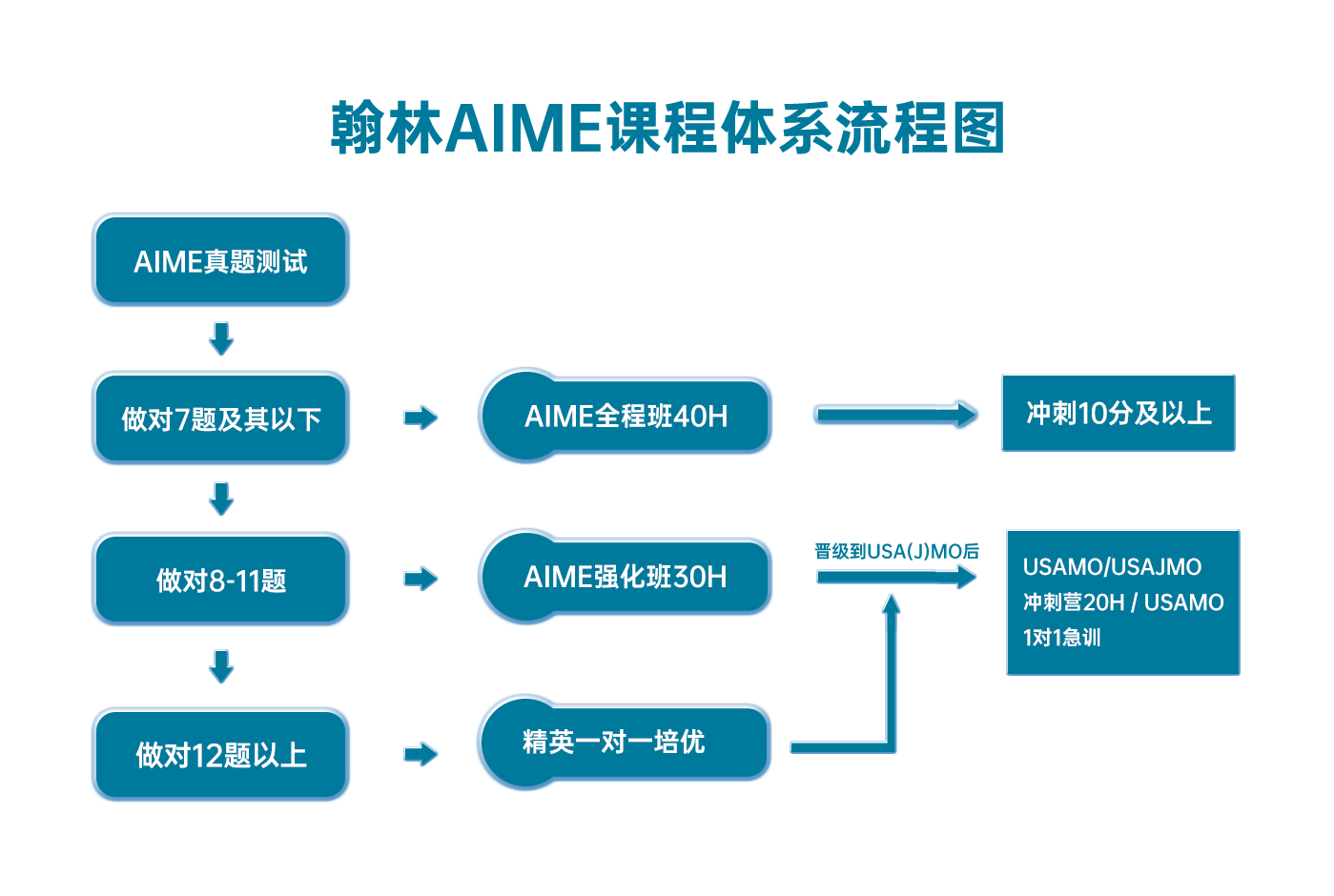
翰林AIME课程体系流程图

最新发布
© 2026. All Rights Reserved. 沪ICP备2023009024号-1









