翰林国际教育,国内国际竞赛领域的开拓者与引领者。我们不仅是系统辅导与深度教研的先行者,更为整个行业提供权威的赛事资讯与海量真题讲义。在数学、物理、化学、生物、计算机、商科、数模等核心领域,我们的战绩长期稳居头部领先地位,屡屡斩获国家队级别最高荣誉。作为同时拥有学科培训、AP国际学校及美高资质的权威教育组织,我们为学生提供一站式的卓越培养体系,助力英才迈向世界顶尖学府。
一、体制内升学:中考与高考中的“差异化竞争力”
中考强基计划中的核心参考价值
国内顶尖中学的“强基计划”旨在选拔具有理科潜力的学生,AMC10成绩成为评估数学能力的关键指标。例如,北京人大附中、上海华师大二附中等学校在理科实验班招生中,明确将AMC10奖项作为面试准入条件。全球排名前5%的获奖者可直接获得面试资格,无需经过初试筛选。这一政策表明,AMC10成绩不仅代表学生的数学水平,更被视为综合素质的体现。强基计划通过此类竞赛筛选学生,旨在快速识别具备高阶思维能力的潜质人才。
高考综合评价中的“学术特长”认证
在高考多元录取机制下,复旦大学、上海交通大学等高校在综合评价招生中,将AMC10奖项作为学术能力的补充证明。获奖学生可部分替代传统学科竞赛成绩(如数学联赛),成为“学术特长生”的重要标签。尤其在江浙沪地区的综评体系中,AMC10全球前2.5%的奖项被视为省级数学竞赛二等奖同等含金量,可直接在申请材料中凸显学生的数学优势。这一趋势反映了国内高校对国际化竞赛标准的接纳,以及对跨学科思维能力的重视。
竞赛背景对学科竞争力的长期增益
体制内学生若在AMC10中晋级AIME(美国数学邀请赛),其数学思维深度将显著超越同龄人。AMC10的命题逻辑强调抽象推理与问题建模能力,这与国内数学联赛、物理竞赛的考察方向高度契合。获奖学生在后续竞赛中(如全国高中数学联赛)往往表现更突出,因其已适应高难度、多变式的解题环境。此外,AMC10的训练能提升学生的逻辑严谨性与计算效率,间接助力高考数学压轴题的攻克。
二、体制外升学:海外名校的“隐性筛选标准”
美国本科申请中的学术能力背书
麻省理工学院(MIT)、加州理工学院等顶尖理工院校在申请系统中明确建议提交AMC10成绩。尽管列为“可选”,但实际录取数据表明,全球前1%的获奖者中约有30%最终进入TOP20美国高校。这些学校将AMC10成绩视为数学潜力的核心指标,其含金量可直接对标中国数学奥林匹克(CMO)省级一等奖。尤其对于申请工程、计算机等专业的学生,AMC10高分可弥补SAT/ACT数学分数的单一性,证明其思维层次远超标准化考试范围。
英国G5高校的专业能力评估工具
牛津大学、剑桥大学的数学与计算机专业常在面试中使用AMC10真题测试学生反应速度与思维延展性。帝国理工学院则直接在申请指南中注明,AMC10成绩可作为“学术潜力证明”替代部分笔试成绩。英国高校重视竞赛成绩的原因在于,AMC10的题目设计强调逻辑链条的完整性与非标准解法,这与英国精英教育中的批判性思维要求高度一致。获奖者在面试中更易展现其适应高强度学术环境的能力。
国际学校入学与课程体系的衔接优势
深国交、上海平和学校等知名国际学校在入学考试中直接采用AMC10原题或改编题,奖项获得者可获优先录取资格。这些学校将AMC10成绩视为学生适应国际课程(如IB、AP微积分)的关键预测指标。据统计,AMC10高分学生在国际课程中的数学科目平均成绩比未参与者高15%以上。此外,AMC10的训练有助于学生提前熟悉西方数学体系的表达方式与论证逻辑,减少未来留学后的学术适应周期。
三、综合价值:超越升学的思维塑造与长远影响
AMC10的含金量不仅体现在升学环节,更在于其对思维模式的深层塑造。其题目设计融合了知识应用与创新探索,要求学生突破模板化解题模式,培养多角度分析问题的能力。这种训练对任何学术方向的学生均有长远价值:体制内学生可提升理科综合素养,体制外学生则能构建与国际教育接轨的思维框架。
不同课程体系学生备考AMC10数学竞赛规划
一、体制内学生:补全竞赛思维,突破“应用题陷阱”
1. 系统性知识补全
使用《奥数教程》等专业竞赛教材,重点学习数论模块(包括质因数分解、同余方程、整数性质)、组合数学(排列组合进阶、容斥原理、鸽巢原理)等AMC10高频考点
每周安排固定时间学习新知识点,并通过配套习题巩固理解,建议每日投入1-2小时专项训练
建立知识图谱,将离散的知识点系统化,形成完整的数学知识体系
2. 思维模式转型训练
从“结果导向”解题转向“过程导向”分析,重点训练反证法、数学归纳法等证明方法
通过AMC10历年真题训练“一题多解”能力,特别是后10道难题的多种解法分析
参加线上竞赛社群,与其他考生交流解题思路,拓宽思维维度
3. 阶梯式真题训练
从AMC8真题入手建立基础,逐步过渡到AMC10早期真题,最后挑战近年高难度真题
重点分析2015年后的AMC10真题,总结后10道题的出题规律和解题技巧
掌握“设数法”、“度量法”、“极端原理”等快速解题技巧,提高解题效率
4. 应试策略优化
模拟真实考试环境,每周末进行全真模考,训练时间分配能力
前15题控制在40分钟内完成,后10题留出35分钟深度思考
建立错题本系统,定期复盘错误原因,避免同类错误重复发生
二、IB体系学生:深化HL课程,填补“知识断层”
1. 针对性知识补充
使用《Introduction to Number Theory》系统学习数论基础,重点掌握模运算、狄利克雷特征等概念
通过《Geometry Revisited》深化几何理解,特别是圆的性质、三角形几何和几何变换
将IB知识体系与AMC10考点对接,例如用IB概率知识解决AMC10中的概率问题
2. 真题模拟与时间管理
每周完成1套完整的AMC10限时模拟,严格遵循75分钟的时间限制
训练“跳题策略”:遇到卡壳超过3分钟的题目立即跳过,确保完成所有力所能及的题目
使用计时器分段控制:前10题(20分钟)、中间10题(25分钟)、后5题(30分钟)
3. 跨学科能力整合
将IB物理中的力学问题转化为数学模型,如用微积分求解极值问题
利用IB的TOK(知识论)训练批判性思维,提高对数学问题本质的理解
建立数学建模思维,将实际问题抽象为数学问题,这也是IB评估的重要能力
4. 资源优化利用
充分利用IB学校的国际资源,获取AMC10官方备考材料
参加校内数学社团或创建学习小组,通过同伴学习提高备考效率
利用IB假期时间参加专项培训营,集中突破薄弱环节
三、A-Level体系学生:查漏补缺,避开“微积分误区”
1. 基础能力强化
使用《Algebra and Trigonometry》巩固代数基础,重点训练多项式因式分解、余数定理、二次函数性质等
补充几何构造训练,特别是平面几何的证明方法和立体几何的空间想象能力
通过Khan Academy等在线平台弥补知识漏洞,建立完整的知识体系
2. 错题管理系统
建立电子化错题本,按知识点分类记录错误题目
标注错误类型:计算错误、概念错误、思路错误等,针对性改进
每周回顾错题,确保同类错误不再发生
3. 解题技巧专项训练
掌握“排除法”、“特殊值法”、“选项代入法”等快速解题技巧
4. 备考节奏规划
提前3-6个月开始系统备考,分阶段制定学习目标
第一阶段(1-2个月):知识点全面覆盖
第二阶段(1-2个月):真题分类训练
第三阶段(1个月):全真模考与弱点强化
最终阶段(2周):心理调整与策略优化
四、AP体系学生:知识迁移,发挥“微积分优势”
1. 前置知识拓展
提前完成AP微积分基础内容,为后续晋级AIME做准备
重点训练“微积分与数列结合”的题型,这是AMC10到AMC12的过渡重点
2. 跨学科应用训练
将微积分思想应用于AMC10最值问题,如几何面积优化、函数极值求解
用数列知识解决“递推关系”问题,这是AMC10的常见题型
3. 综合能力提升
a. 每周完成2套真题模拟,注重质量而非数量,深度分析每道题的多种解法
b. 参加线上竞赛课程,学习专业竞赛教师的解题技巧和思维方法
c. 建立解题思维框架:问题分析→方法选择→过程实施→结果验证
4. 长期发展规划
将AMC10作为起点,规划AMC12→AIME→USAMO的晋级路径
利用AP微积分基础,提前学习多元微积分和线性代数,为更高层次竞赛做准备
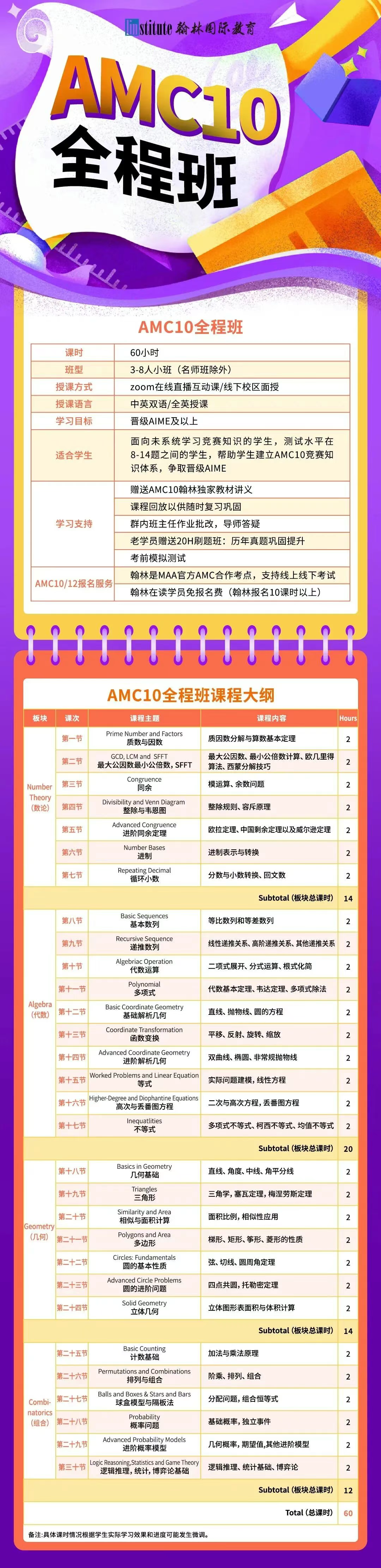
翰林AMC10培训班
翰林AMC10培训班