从勾股定理的不同证明方法看代数与几何的比较

勾股定理的多种证明方法各具特色，尤其是欧几里得的几何证明方法与代数证明方法之间的对比，展现了数学思维的多样性。本文将深入探讨这两种证明方法的特点及其在学习过程中的应用。

欧几里得的几何证明方法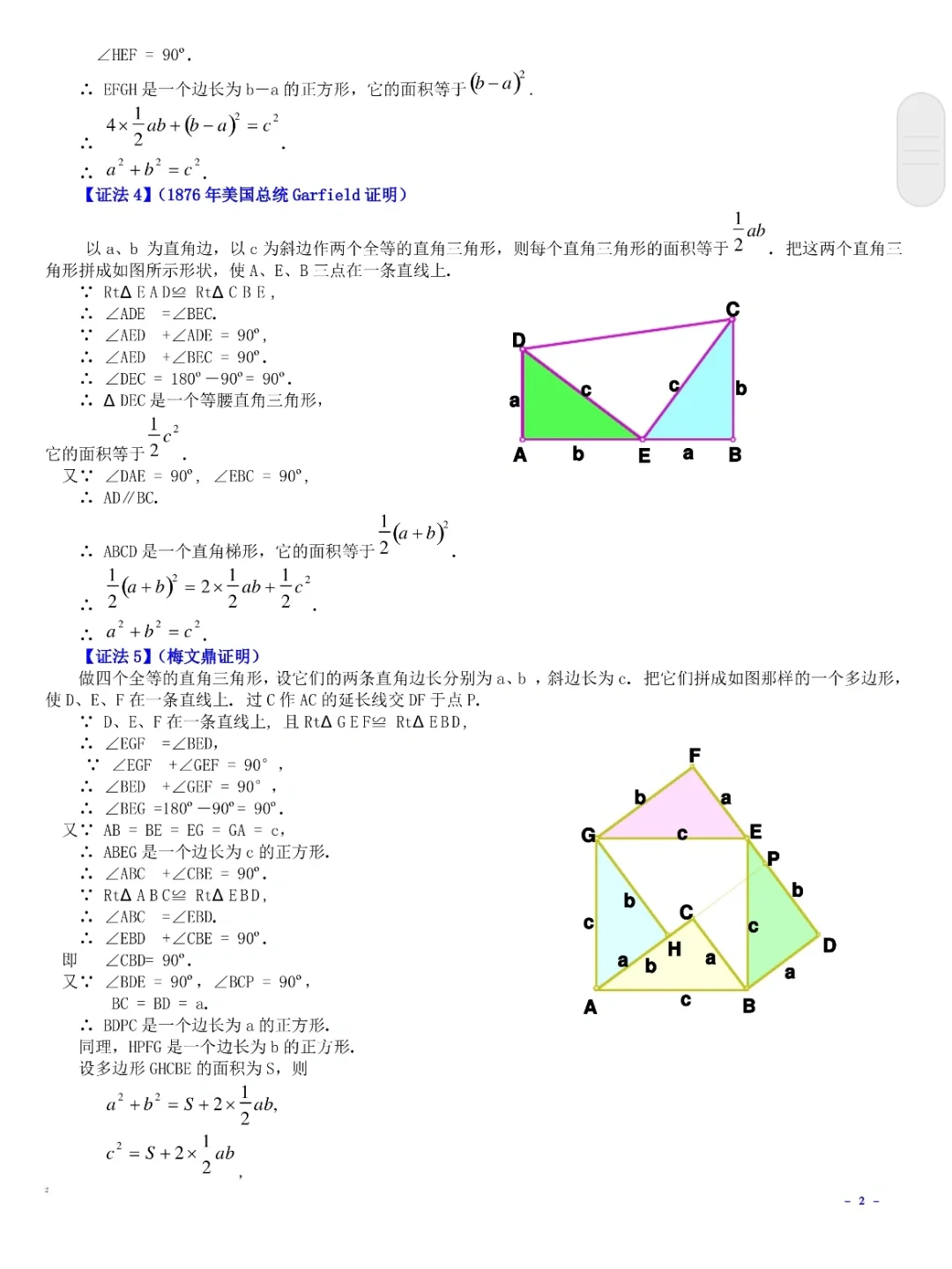

欧几里得的证明方法以其严谨性和逻辑性著称，主要依赖于几何图形的性质。其基本思路是通过寻找相等的线段和角，来证明三角形的全等性，并由此建立等量关系。具体步骤包括：

• 构造图形：在直角三角形中添加辅助线，形成新的几何图形。
• 证明全等：使用边角边（SAS）、角边角（ASA）等全等条件，证明所构造的三角形全等。
• 建立等量关系：通过全等三角形的性质，得出勾股定理的结论。

这种方法虽然严谨，但在辅助线的构造上往往需要灵活的思维和丰富的几何直觉。初学者在学习过程中，常常会遇到难以想到合适辅助线的困扰，这就需要较高的空间想象力和逻辑推理能力。

代数证明方法的简单明了

相比之下，代数证明方法如赵爽弦图和总统法则则显得简单明了。其核心在于设未知量并寻找等量关系，具体步骤如下：

• 设未知数：在证明过程中，设定多个未知数，构建代数方程。
• 寻找等量关系：通过已知条件和设定的未知数，建立等量关系，形成方程。
• 代数化简：通过基本的代数运算，将方程化简，最终得出勾股定理。

代数证明方法的优势在于其直接性和灵活性。只要敢于设定未知数，思路就会变得清晰明了。代数方法不仅降低了思维的复杂度，还能帮助学生在解题过程中建立自信。

结论

从勾股定理的不同证明方法中，我们可以看到几何与代数的各自特点。欧几里得的几何证明方法强调逻辑严谨性和空间想象力，而代数证明方法则以其简单明了的思路吸引人。对于初学者而言，掌握代数证明方法可以为理解几何概念打下良好的基础，同时也能增强解决问题的信心。

希望通过对这两种证明方法的比较，能够帮助学生更好地理解勾股定理，并在学习过程中找到适合自己的思维方式。