初中几何之勾股定理的六种常见证明方法

勾股定理作为几何计算中的重要定理，其地位无可撼动。它不仅在数学中占据重要位置，也是许多实际问题解决的基础。随着历史的发展，勾股定理的证明方法也不断丰富，至今已有近十种之多。本文将为大家详细介绍六种常见的证明方法，帮助初学者深入理解勾股定理的本质。

什么是勾股定理？

勾股定理是指在直角三角形中，直角两边的平方和等于斜边的平方。用公式表示为：

其中，$a$ 和 $b$ 为直角边，$c$ 为斜边。理解这一关系是学习几何的重要基础。

六种常见证明方法

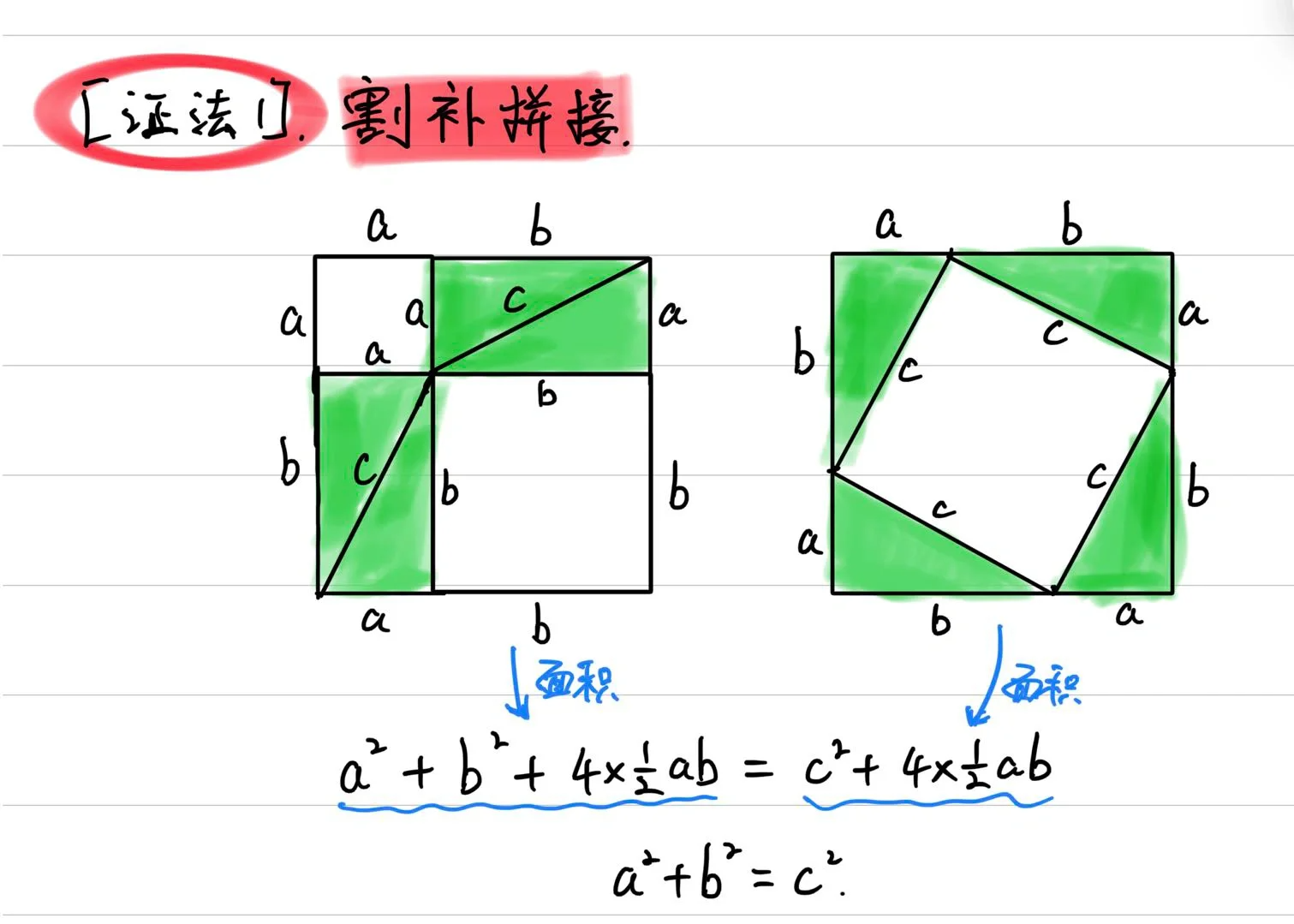
1. 割补拼接法

割补拼接法是通过将直角三角形分割成不同的部分，重新拼接来证明勾股定理。这种方法直观易懂，适合初学者。具体步骤如下：

• 将直角三角形的两条直角边分别延长，形成一个大正方形。
• 在这个大正方形内部，拼接出两个小正方形，分别对应于直角边的平方。
• 通过计算大正方形和小正方形的面积关系，得出勾股定理的结论。

2. 内弦图法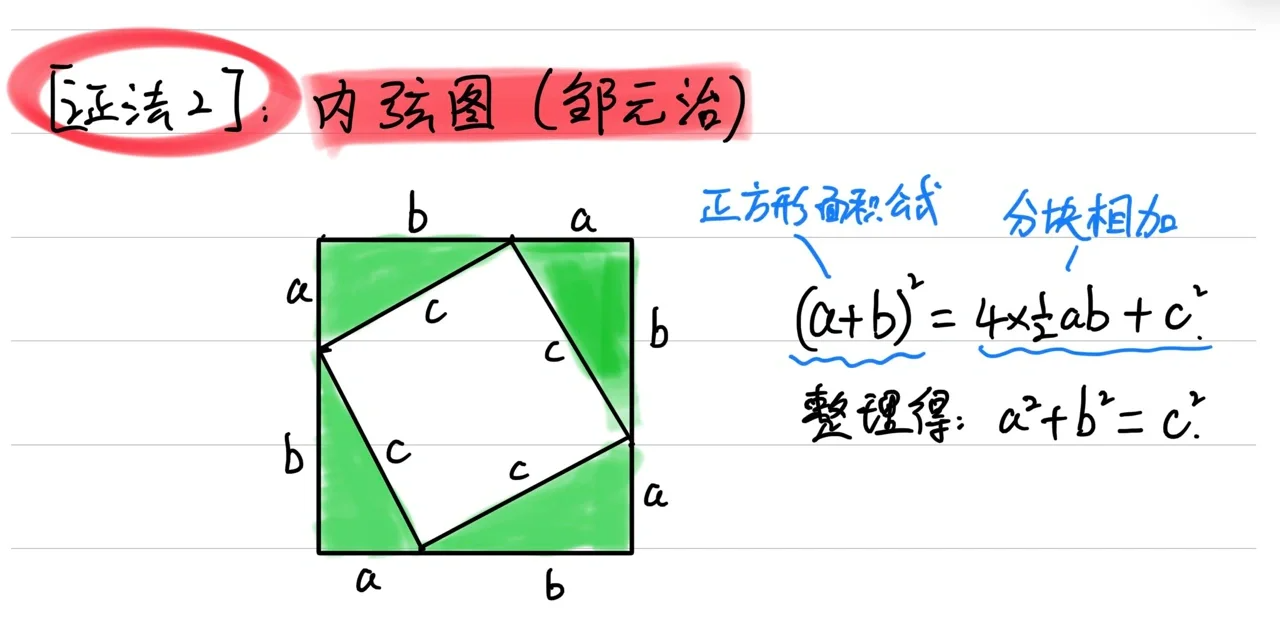

内弦图法利用几何图形的对称性进行证明。具体步骤为：

• 在直角三角形内部画出一个内切圆。
• 通过分析内切圆与三角形各边的关系，推导出面积的变化。
• 最终得出直角边平方和等于斜边平方的结论。

3. 外弦图法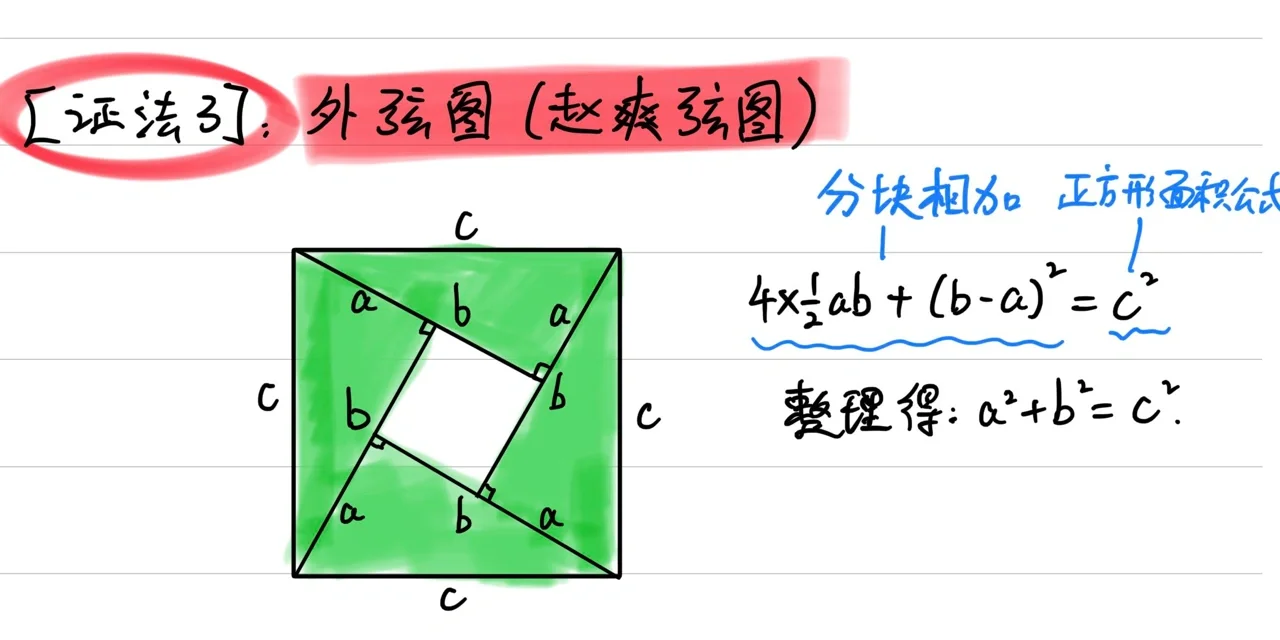

外弦图法与内弦图法相对，通过外部图形的构建进行证明。步骤如下：

• 在直角三角形外部构建一个外接圆。
• 通过分析外接圆的弦长与三角形各边的关系，推导出面积之间的关系。
• 最终得出勾股定理的结论。

4. 总统证法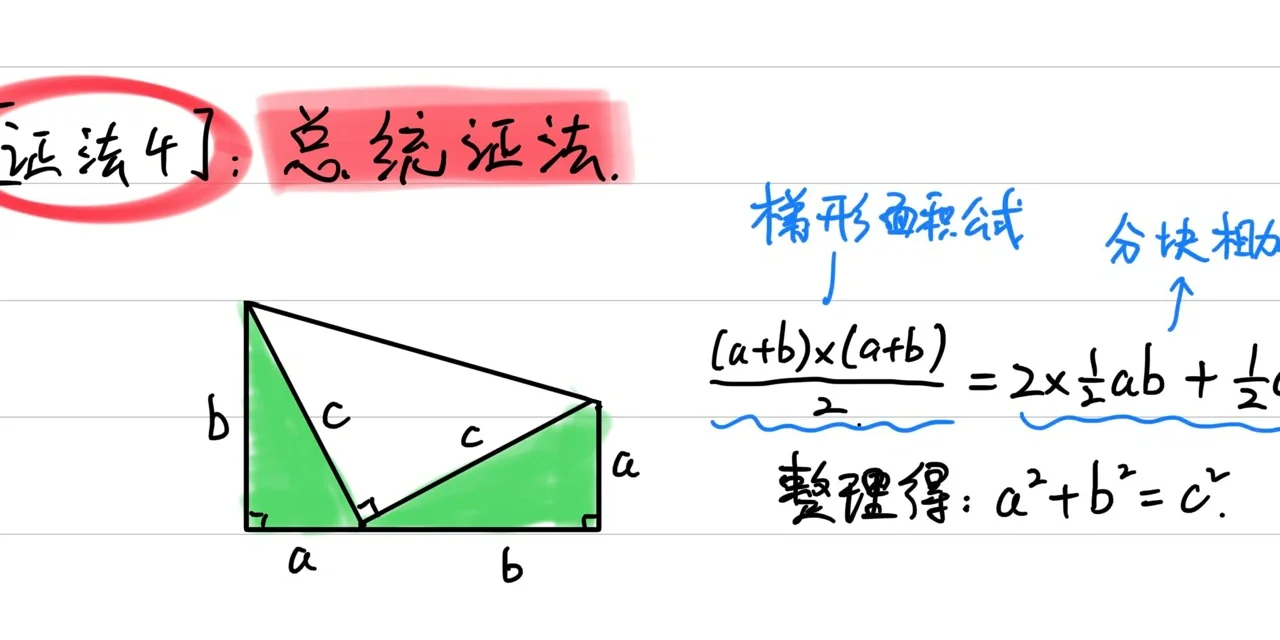

总统证法以其独特的几何构造而闻名。具体步骤为：

• 选取一个直角三角形，在其周围构建一个大的正方形。
• 将直角三角形的三个顶点分别与正方形的边相连，形成新的图形。
• 通过计算新图形的面积，推导出勾股定理的关系。

5. 青朱出入图法

青朱出入图法通过图形的动态变化进行证明。具体步骤为：

• 在直角三角形中引入青朱的概念，通过图形的变化展示面积的转化。
• 通过对比不同形状的面积，得出直角边平方和等于斜边平方的结论。

6. 欧几里得证法

欧几里得证法是最经典的证明方法之一，步骤如下：

• 通过构造一个正方形，并在其内部放置直角三角形。
• 通过对比正方形的面积与直角三角形的面积，推导出勾股定理的结论。

结语

勾股定理的多种证明方法不仅丰富了我们的数学知识，也帮助我们更好地理解几何图形之间的关系。初学者在学习过程中，理解这些证明方法的本质，即“几何图形面积之间的变形转化”，将有助于更深入掌握勾股定理。

希望今天的分享能对大家的学习有所帮助。如果你喜欢这篇文章，欢迎关注、点赞和转发，让我们一起在数学的道路上不断进步！