- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Maths: Pure:复习笔记9.1.1 Parametric Equations - Basics
Parametric Equations - Basics
What are parametric equations?
- Graphs are usually described by a Cartesian equation
- The equation involves x and y only
- Equations like this can sometimes be rearranged into the form, y = f(x)
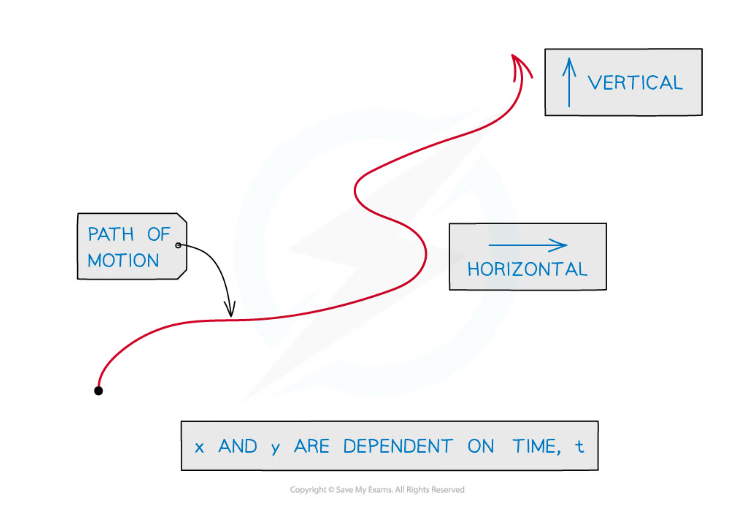
- In parametric equations both x and y are dependent on a third variable
- This is called a parameter
- t and θ are often used as parameters
- A common example …
- x is the horizontal position of an object
- y is the vertical position of an object
- and the position of the object is dependent on time t
- x is a function of t, y is a function of t
- x = f(t)
- y = g(t)
What do I do with parametric equations?
- It is still possible to plot a graph of y against x from their parametric equations
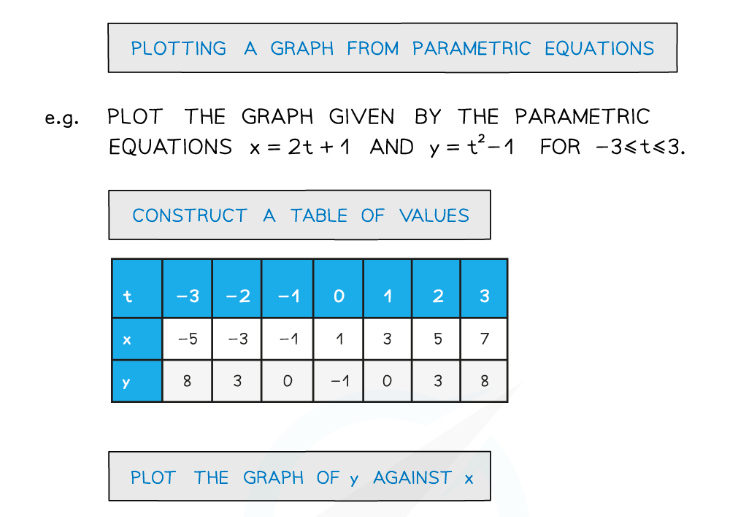
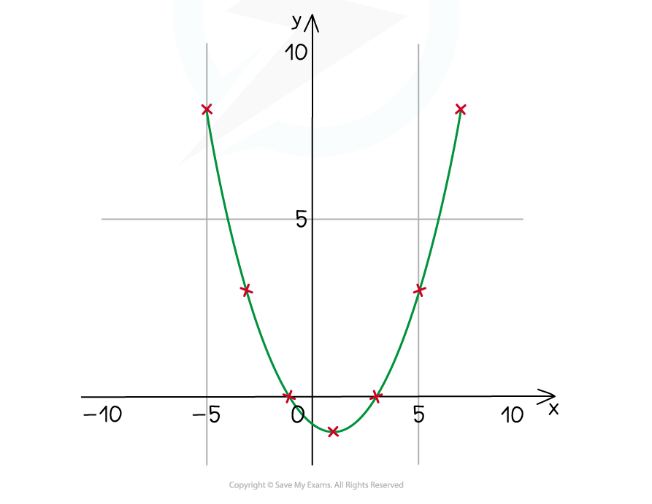
- Also see Parametric Equations – Sketching Graphs
What is the link between parametric equations and circles?
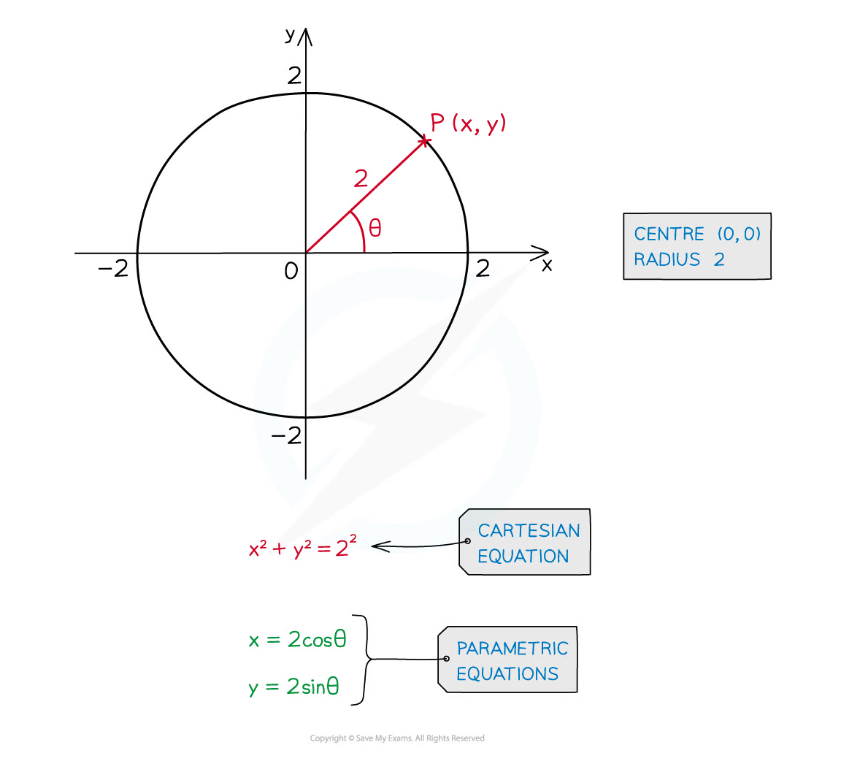
- For a circle, centre (0, 0) and radius r
- x = rcos θ
- y = rsin θ
- (Note that r is constant, this is not two parameters)
- For a circle, centre (a, b) and radius r
- x = rcos θ + a
- y = rsin θ + b
Worked Example
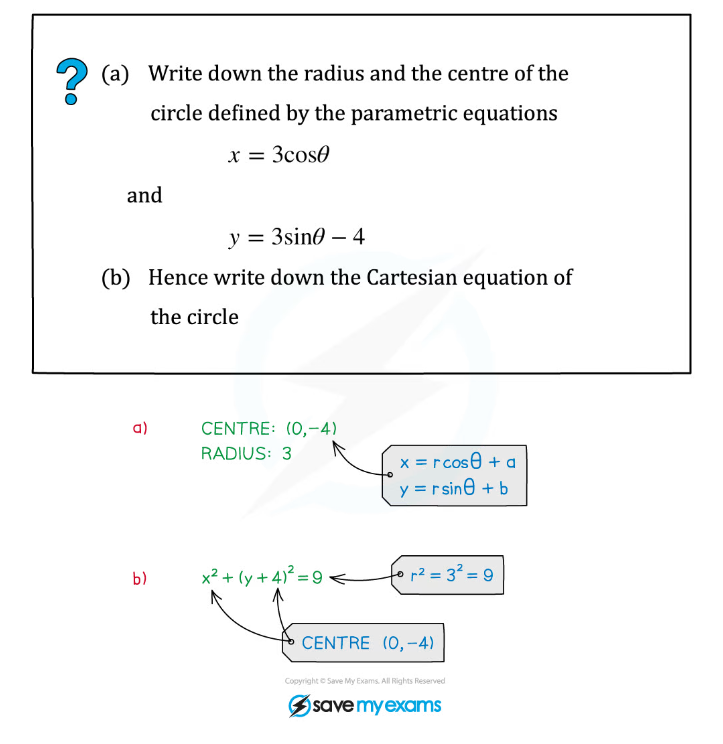
转载自savemyexams

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









