CIE A Level Maths: Pure 3复习笔记3.4.1 Trigonometric Proof
Trigonometric Proof
Proving trigonometric identities
- You can use trigonometric identities you already know to prove new identities
- Make sure you know the simple trigonometric identities and further trigonometric identities
- To prove an identity start on one side and proceed step by step until you get to the other side
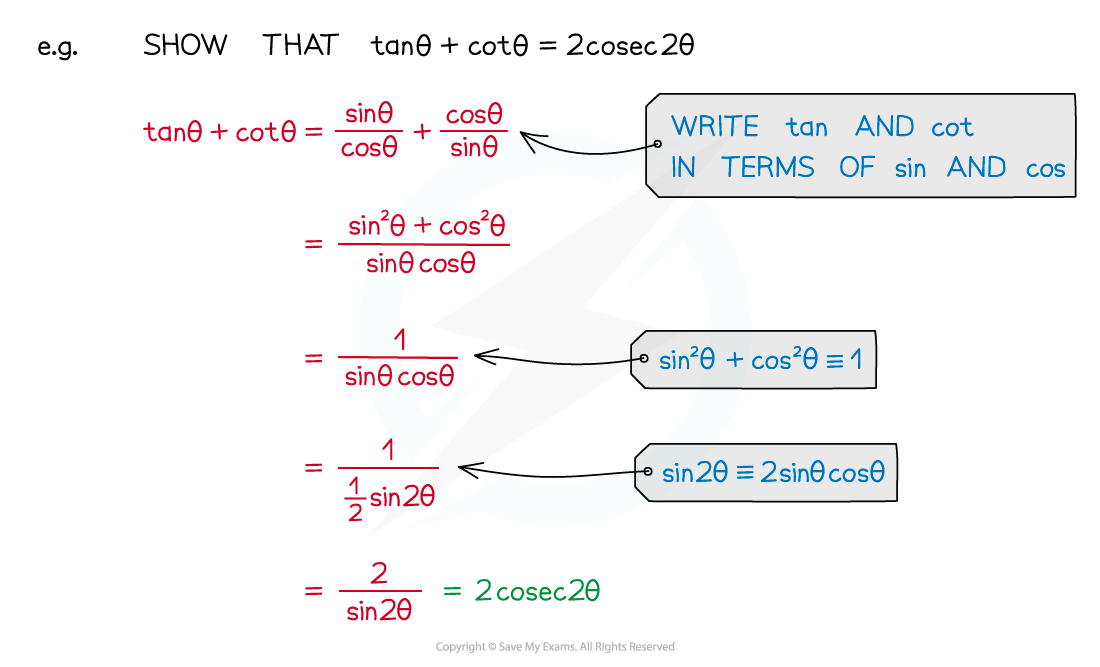
- Clever substitution into the compound angle formulae can be a useful tool for proving identities
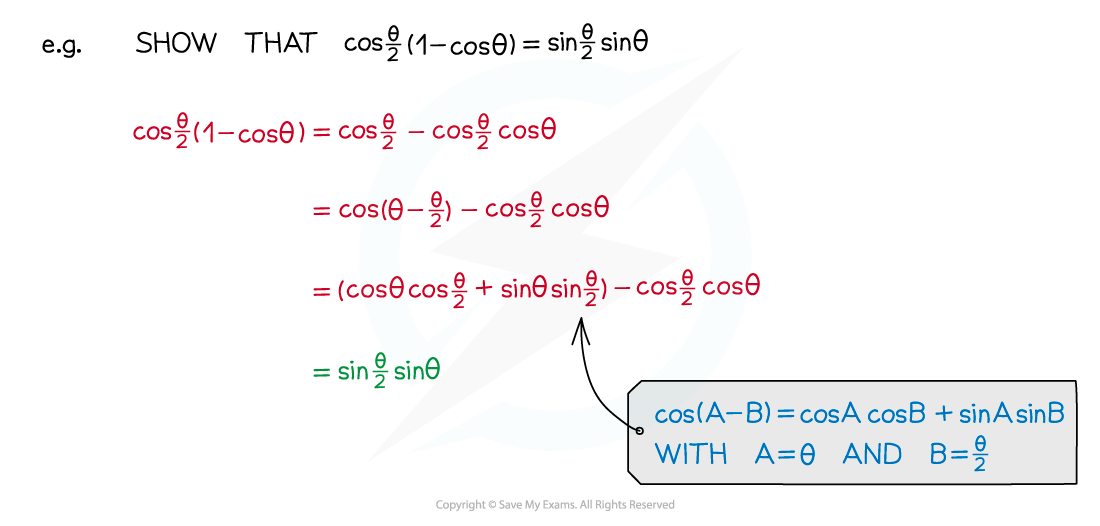
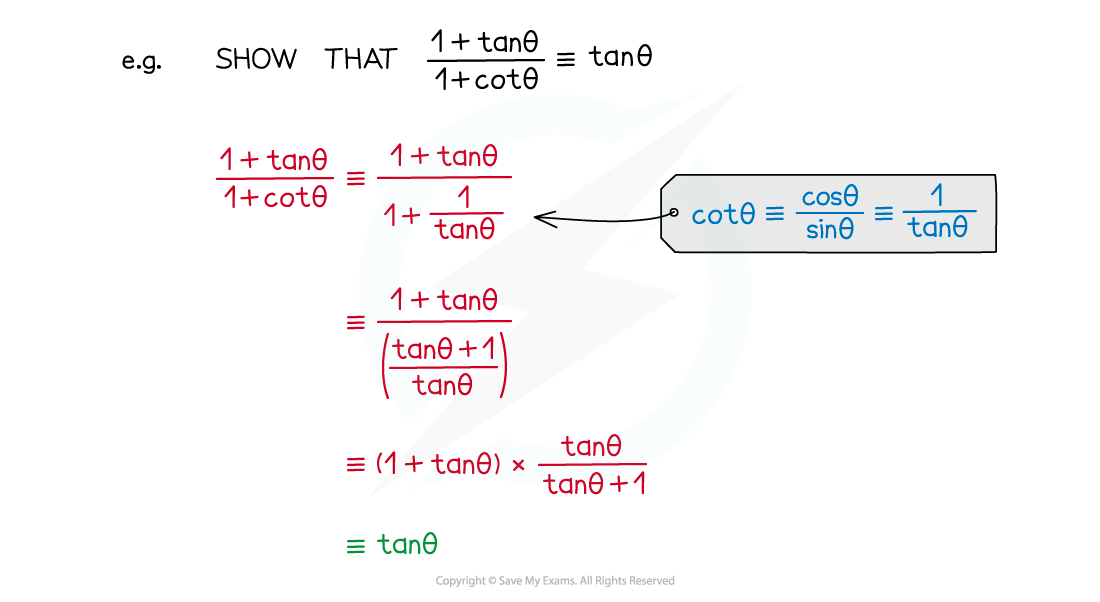
- Make sure you are confident handling fractions and fractions-within-fractions
- Always keep an eye on the 'target' expression – this can help suggest what identities to use
Exam Tip
- Don't forget that you can start a proof from either end – sometimes it might be easier to start from the right-hand side (see the Worked Example)
- A number of trigonometric identities are given to you in the formulae booklet – make sure you know which ones are (and aren't) in there
Worked Example
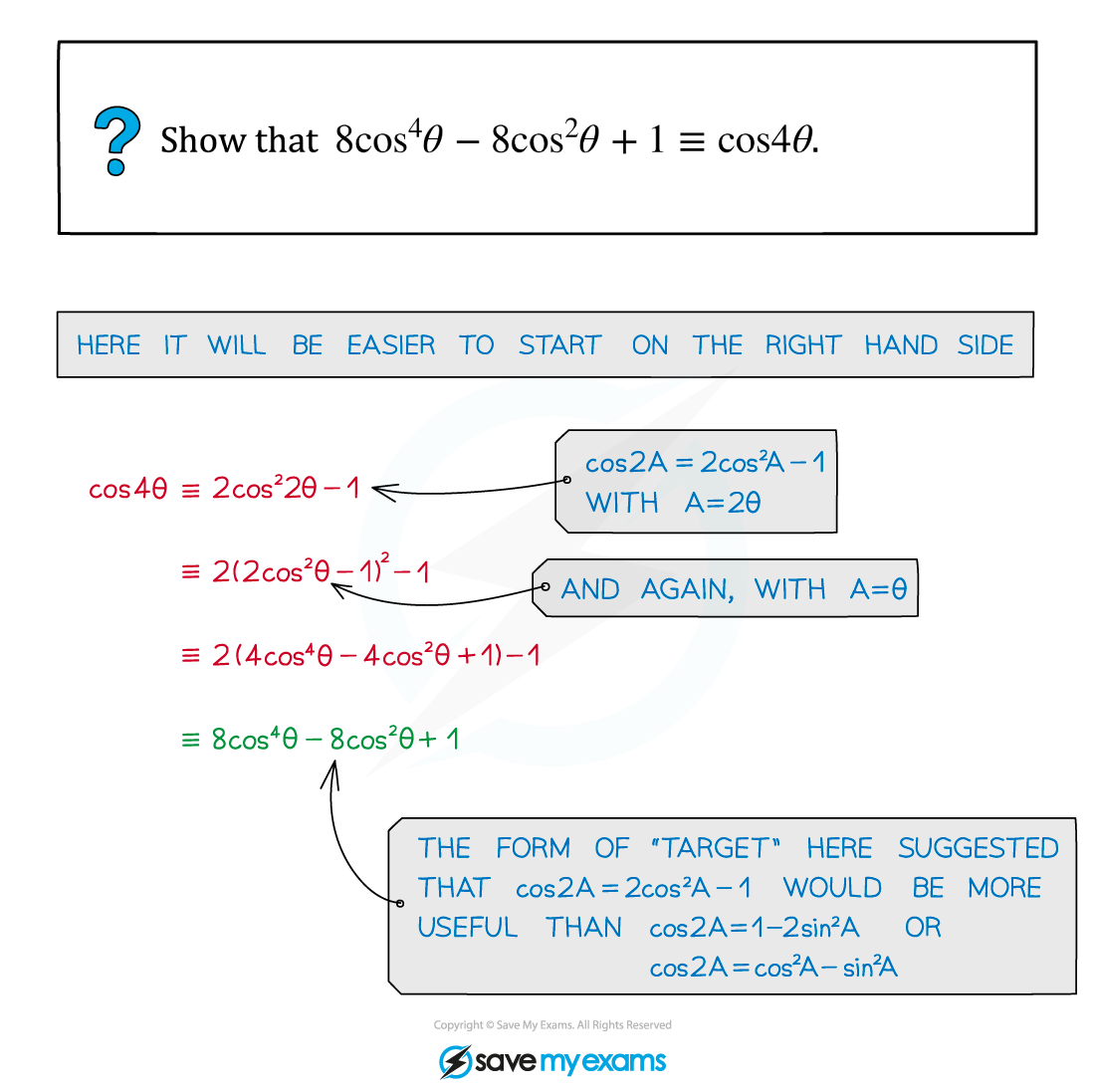
转载自savemyexams
翰林AMC8视频课重磅上线！
国际竞赛真题资源免费领取
