美国数学竞赛答案解析 2017 AMC 10B 22-25

美国数学学术活动答案解析

2017 AMC 10B 22-25

Problem 22

The diameter of a circle of radius is extended to a point outside the circle so that . Point is chosen so that and line is perpendicular to line . Segment intersects the circle at a point between and . What is the area of ?

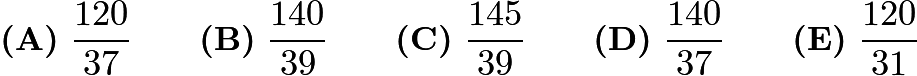
Problem 23

Let be the -digit number that is formed by writing the integers from to in order, one after the other. What is the remainder when is divided by ?

Problem 24

The vertices of an equilateral triangle lie on the hyperbola , and a vertex of this hyperbola is the centroid of the triangle. What is the square of the area of the triangle?

Problem 25

Last year Isabella took math tests and received different scores, each an integer between and , inclusive. After each test she noticed that the average of her test scores was an integer. Her score on the seventh test was . What was her score on the sixth test?

1. Notice that 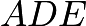and 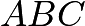are right triangles. Then 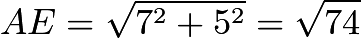. 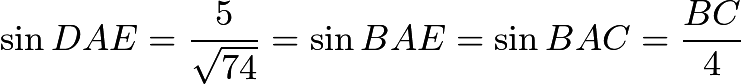, so 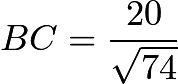. We also find that 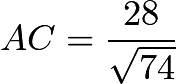, and thus the area of 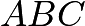is .
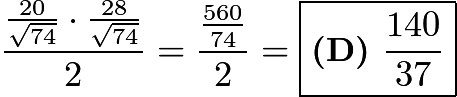2. We only need to find the remainders of N when divided by 5 and 9 to determine the answer. By inspection, 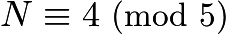. The remainder when 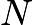is divided by 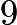is 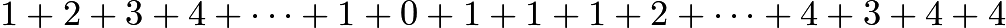, but since 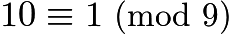, we can also write this as 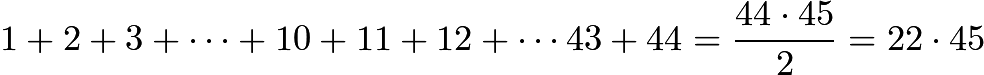, which has a remainder of 0 mod 9. Therefore, by inspection, the answer is 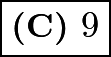.Note: the sum of the digits of 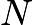is .
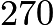3. WLOG, let the centroid of 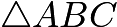be 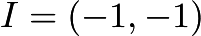. The centroid of an equilateral triangle is the same as the circumcenter. It follows that the circumcircle must intersect the graph exactly three times. Therefore, 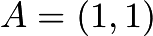, so 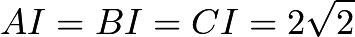, so since 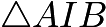is isosceles and 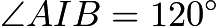, then by Law of Cosines, 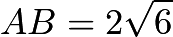. Therefore, the area of the triangle is 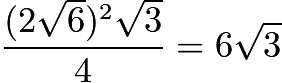, so the square of the area of the triangle is .
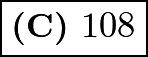4. Let the sum of the scores of Isabella's first 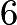tests be 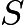. Since the mean of her first 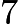scores is an integer, then 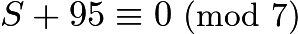, or 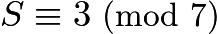. Also, 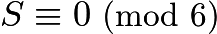, so by CRT, 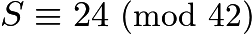. We also know that 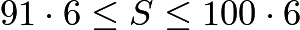, so by inspection, 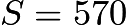. However, we also have that the mean of the first 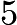integers must be an integer, so the sum of the first 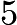test scores must be an multiple of 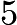, which implies that the 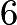th test score is .

 

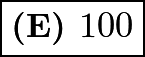以上解析方式仅供参考

更多详细解析方式，请联系小助手了解更多