Home » 国际竞赛 » 数学国际竞赛 » AMC美国数学竞赛 » Details

1989AIME 真题及答案解析

Category: AMC美国数学竞赛, 国际竞赛 Date: 2019年12月12日上午11:38

1989AIME 真题及答案解析

答案解析请参考文末

Problem 1

Compute $sqrt{(31)(30)(29)(28)+1}$ .

Problem 2

Ten points are marked on a circle. How many distinct convex polygons of three or more sides can be drawn using some (or all) of the ten points as vertices?

Problem 3

Suppose $n_{}^{}$ is a positive integer and $d_{}^{}$ is a single digit in base 10. Find $n_{}^{}$ if

$frac{n}{810}=0.d25d25d25ldots$

Problem 4

If $a<b<c<d<e^{}_{}$ are consecutive positive integers such that $b+c+d^{}_{}$ is a perfect square and $a+b+c+d+e^{}_{}$ is a perfect cube, what is the smallest possible value of $c^{}_{}$ ?

Problem 5

When a certain biased coin is flipped five times, the probability of getting heads exactly once is not equal to $0^{}_{}$ and is the same as that of getting heads exactly twice. Let $frac ij^{}_{}$ , in lowest terms, be the probability that the coin comes up heads in exactly $3_{}^{}$ out of $5^{}_{}$ flips. Find $i+j^{}_{}$ .

Problem 6

Two skaters, Allie and Billie, are at points $A^{}_{}$ and $B^{}_{}$ , respectively, on a flat, frozen lake. The distance between $A^{}_{}$ and $B^{}_{}$ is $100^{}_{}$ meters. Allie leaves $A^{}_{}$ and skates at a speed of $8^{}_{}$ meters per second on a straight line that makes a $60^circ$ angle with $AB^{}_{}$ . At the same time Allie leaves $A^{}_{}$ , Billie leaves $B^{}_{}$ at a speed of $7^{}_{}$ meters per second and follows the straight path that produces the earliest possible meeting of the two skaters, given their speeds. How many meters does Allie skate before meeting Billie?

AIME 1989 Problem 6.png

Problem 7

If the integer $k^{}_{}$ is added to each of the numbers $36^{}_{}$ , $300^{}_{}$ , and $596^{}_{}$ , one obtains the squares of three consecutive terms of an arithmetic series. Find $k^{}_{}$ .

Problem 8

Assume that $x_1,x_2,ldots,x_7$ are real numbers such that

$x_1+4x_2+9x_3+16x_4+25x_5+36x_6+49x_7=1^{}_{}$ $4x_1+9x_2+16x_3+25x_4+36x_5+49x_6+64x_7=12^{}_{}$ $9x_1+16x_2+25x_3+36x_4+49x_5+64x_6+81x_7=123^{}_{}$ Find the value of $16x_1+25x_2+36x_3+49x_4+64x_5+81x_6+100x_7^{}$ .

Problem 9

One of Euler's conjectures was disproved in the 1960s by three American mathematicians when they showed there was a positive integer $n$ such that $133^5+110^5+84^5+27^5=n^{5}_{}$ . Find the value of $n^{}_{}$ .

Problem 10

Let $a_{}^{}$ , $b_{}^{}$ , $c_{}^{}$ be the three sides of a triangle, and let $alpha_{}^{}$ , $beta_{}^{}$ , $gamma_{}^{}$ , be the angles opposite them. If $a^2+b^2=1989^{}_{}c^2$ , find

$frac{cot gamma}{cot alpha+cot beta}$

Problem 11

A sample of 121 integers is given, each between 1 and 1000 inclusive, with repetitions allowed. The sample has a unique mode (most frequent value). Let $D^{}_{}$ be the difference between the mode and the arithmetic mean of the sample. What is the largest possible value of $lfloor D^{}_{}rfloor$ ? (For real $x^{}_{}$ , $lfloor x^{}_{}rfloor$ is the greatest integer less than or equal to $x^{}_{}$ .)

Problem 12

Let $ABCD^{}_{}$ be a tetrahedron with $AB=41^{}_{}$ , $AC=7^{}_{}$ , $AD=18^{}_{}$ , $BC=36^{}_{}$ , $BD=27^{}_{}$ , and $CD=13^{}_{}$ , as shown in the figure. Let $d^{}_{}$ be the distance between the midpoints of edges $AB^{}_{}$ and $CD^{}_{}$ . Find $d^{2}_{}$ .

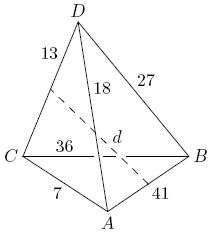
AIME 1989 Problem 12.png

Problem 13

Let $S^{}_{}$ be a subset of ${1,2,3^{}_{},ldots,1989}$ such that no two members of $S^{}_{}$ differ by $4^{}_{}$ or $7^{}_{}$ . What is the largest number of elements $S^{}_{}$ can have?

Problem 14

Given a positive integer $n^{}_{}$ , it can be shown that every complex number of the form $r+si^{}_{}$ , where $r^{}_{}$ and $s^{}_{}$ are integers, can be uniquely expressed in the base $-n+i^{}_{}$ using the integers $1,2^{}_{},ldots,n^2$ as digits. That is, the equation

$r+si=a_m(-n+i)^m+a_{m-1}(-n+i)^{m-1}+cdots +a_1(-n+i)+a_0$ is true for a unique choice of non-negative integer $m^{}_{}$ and digits $a_0,a_1^{},ldots,a_m$ chosen from the set ${0^{}_{},1,2,ldots,n^2}$ , with $a_mne 0^{}){}$ . We write

$r+si=(a_ma_{m-1}ldots a_1a_0)_{-n+i}$ to denote the base $-n+i^{}_{}$ expansion of $r+si^{}_{}$ . There are only finitely many integers $k+0i^{}_{}$ that have four-digit expansions

$k=(a_3a_2a_1a_0)_{-3+i^{}_{}}~~~~a_3ne 0.$ Find the sum of all such $k^{}_{}$ .

Problem 15

Point $P^{}_{}$ is inside $triangle ABC^{}_{}$ . Line segments $APD^{}_{}$ , $BPE^{}_{}$ , and $CPF^{}_{}$ are drawn with $D^{}_{}$ on $BC^{}_{}$ , $E^{}_{}$ on $AC^{}_{}$ , and $F{}{}^{}_{}$ on $AB^{}_{}$ (see the figure at right). Given that $AP=6^{}_{}$ , $BP=9^{}_{}$ , $PD=6^{}_{}$ , $PE=3^{}_{}$ , and $CF=20^{}_{}$ , find the area of $triangle ABC^{}_{}$ .

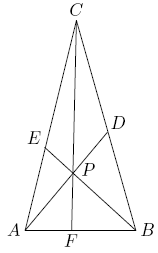
AIME 1989 Problem 15.png

1989AIME 详细解析

Notice ${31*28 = 868}$ and ${30*29 =870}$ . So now our expression is $sqrt{(870)(868) + 1}$ . Setting 870 equal to $y$ , we get $sqrt{(y-1)^{2}}$ which then equals ${(y-1)}$ . So since ${y = 870}$ , ${y-1}=869$ , our answer is $boxed{869}$ .
Any subset of the ten points with three or more members can be made into exactly one such polygon. Thus, we need to count the number of such subsets. There are $2^{10} = 1024$ total subsets of a ten-member set, but of these ${10 choose 0} = 1$ have 0 members, ${10 choose 1} = 10$ have 1 member and ${10 choose 2} = 45$ have 2 members. Thus the answer is $1024 - 1 - 10 - 45 = boxed{968}$ .Note ${n choose 0}+{n choose 1} + {n choose 2} + dots + {n choose n}$ is equivalent to $2^n$
Repeating decimals represent rational numbers. To figure out which rational number, we sum an infinite geometric series, $0.d25d25d25ldots = sum_{i = 1}^infty frac{d25}{1000^n} = frac{100d + 25}{999}$ . Thus $frac{n}{810} = frac{100d + 25}{999}$ so $n = 30frac{100d + 25}{37} =750frac{4d + 1}{37}$ . Since 750 and 37 are relatively prime, $4d + 1$ must be divisible by 37, and the only digit for which this is possible is $d = 9$ . Thus $4d + 1 = 37$ and $n = boxed{750}$ .(Note: Any repeating sequence of $n$ digits that looks like $0.a_1a_2a_3...a_{n-1}a_na_1a_2...$ can be written as $frac{a_1a_2...a_n}{10^n-1}$ , where $a_1a_2...a_n$ represents an $n$ digit number.)
Since the middle term of an arithmetic progression with an odd number of terms is the average of the series, we know $b + c + d = 3c$ and $a + b + c + d + e = 5c$ . Thus, $c$ must be in the form of $3 cdot x^2$ based upon the first part and in the form of $5^2 cdot y^3$ based upon the second part, with $x$ and $y$ denoting an integers. $c$ is minimized if it’s prime factorization contains only $3,5$ , and since there is a cubed term in $5^2 cdot y^3$ , $3^3$ must be a factor of $c$ . $3^35^2 = boxed{675}$ , which works as the solution.
Denote the probability of getting a heads in one flip of the biased coin as $h$ . Based upon the problem, note that ${5choose1}(h)^1(1-h)^4 = {5choose2}(h)^2(1-h)^3$ . After canceling out terms, we get $1 - h = 2h$ , so $h = frac{1}{3}$ . The answer we are looking for is ${5choose3}(h)^3(1-h)^2 = 10left(frac{1}{3}right)^3left(frac{2}{3}right)^2 = frac{40}{243}$ , so $i+j=40+243=boxed{283}$ .
Label the point of intersection as $C$ . Since $d = rt$ , $AC = 8t$ and $BC = 7t$ . According to the law of cosines, $[asy] pointpen=black; pathpen=black+linewidth(0.7); pair A=(0,0),B=(10,0),C=16*expi(pi/3); D(B--A); D(A--C); D(B--C,dashed); MP("A",A,SW);MP("B",B,SE);MP("C",C,N);MP("60^{circ}",A+(0.3,0),NE);MP("100",(A+B)/2);MP("8t",(A+C)/2,NW);MP("7t",(B+C)/2,NE); [/asy]$ $begin{align*}(7t)^2 &= (8t)^2 + 100^2 - 2 cdot 8t cdot 100 cdot cos 60^circ 0 &= 15t^2 - 800t + 10000 = 3t^2 - 160t + 2000 t &= frac{160 pm sqrt{160^2 - 4cdot 3 cdot 2000}}{6} = 20, frac{100}{3}.end{align*}$ Since we are looking for the earliest possible intersection, $20$ seconds are needed. Thus, $8 cdot 20 = boxed{160}$ meters is the solution.Alternatively, we can drop an altitude from $C$ and arrive at the same answer.
Call the terms of the arithmetic progression $a, a + d, a + 2d$ , making their squares $a^2, a^2 + 2ad + d^2, a^2 + 4ad + 4d^2$ .We know that $a^2 = 36 + k$ and $(a + d)^2 = 300 + k$ , and subtracting these two we get $264 = 2ad + d^2$ (1). Similarly, using $(a + d)^2 = 300 + k$ and $(a + 2d)^2 = 596 + k$ , subtraction yields $296 = 2ad + 3d^2$ (2).Subtracting the first equation from the second, we get $2d^2 = 32$ , so $d = 4$ . Substituting backwards yields that $a = 31$ and $k = boxed{925}$ .
Notice that because we are given a system of $3$ equations with $7$ unknowns, the values $(x_1, x_2, ldots, x_7)$ are not fixed; indeed one can take any four of the variables and assign them arbitrary values, which will in turn fix the last three.Given this, we suspect there is a way to derive the last expression as a linear combination of the three given expressions. Let the coefficent of $x_i$ in the first equation be $y_i^2$ ; then its coefficients in the second equation is $(y_i+1)^{2}$ and the third as $(y_i+2)^2$ . We need to find a way to sum these to make $(y_i+3)^2$ [this is in fact a specific approach generalized by the next solution below].Thus, we hope to find constants $a,b,c$ satisfying $ay_i^2 + b(y_i+1)^2 + c(y_i+2)^2 = (y_i + 3)^2$ . FOILing out all of the terms, we get $[ay^2 + by^2 + cy^2] + [2by + 4cy] + b + 4c = y^2 + 6y + 9.$ Comparing coefficents gives us the three equation system: $begin{align*}a + b + c &= 1 2b + 4c &= 6 b + 4c &= 9 end{align*}$ Subtracting the second and third equations yields that $b = -3$ , so $c = 3$ and $a = 1$ . It follows that the desired expression is $a cdot (1) + b cdot (12) + c cdot (123) = 1 - 36 + 369 = boxed{334}$ .
Note that $n$ is even, since the $LHS$ consists of two odd and two even numbers. By Fermat's Little Theorem, we know ${n^{5}}$ is congruent to $n$ modulo 5. Hence, $3 + 0 + 4 + 2 equiv npmod{5}$ $4 equiv npmod{5}$ Continuing, we examine the equation modulo 3, $1 - 1 + 0 + 0 equiv npmod{3}$ $0 equiv npmod{3}$ Thus, $n$ is divisible by three and leaves a remainder of four when divided by 5. It's obvious that $n>133$ , so the only possibilities are $n = 144$ or $n geq 174$ . It quickly becomes apparent that 174 is much too large, so $n$ must be $boxed{144}$ .We can cheat a little bit and approximate, since we are dealing with such large numbers. As above, $n^5equiv npmod{5}$ , and it is easy to see that $n^5equiv npmod 2$ . Therefore, $133^5+110^5+84^5+27^5equiv 3+0+4+7equiv 4pmod{10}$ , so the last digit of $n$ is 4.We notice that $133,110,84,$ and $27$ are all very close or equal to multiples of 27. We can rewrite $n^5$ as approximately equal to $27^5(5^5+4^5+3^5+1^5) = 27^5(4393)$ . This means $frac{n}{27}$ must be close to $4393$ .134 will obviously be too small, so we try 144. $left(frac{144}{27}right)^5=left(frac{16}{3}right)^5$ . Bashing through the division, we find that $frac{1048576}{243}approx 4315$ , which is very close to $4393$ . It is clear that 154 will not give any closer of an answer, given the rate that fifth powers grow, so we can safely assume that $boxed{144}$ is the answer.
We can draw the altitude $h$ to $c$ , to get two right triangles. $cot{alpha}+cot{beta}=frac{c}{h}$ , from the definition of the cotangent. From the definition of area, $h=frac{2A}{c}$ , so $cot{alpha}+cot{beta}=frac{c^2}{2A}$ .Now we evaluate the numerator: $[cot{gamma}=frac{cos{gamma}}{sin{gamma}}]$ From the Law of Cosines and the sine area formula, $begin{align*}cos{gamma}&=frac{1988c^2}{2ab} sin{gamma}&= frac{2A}{ab} cot{gamma}&= frac{cos gamma}{sin gamma} = frac{1988c^2}{4A} end{align*}$ Then $frac{cot gamma}{cot alpha+cot beta}=frac{frac{1988c^2}{4A}}{frac{c^2}{2A}}=frac{1988}{2}=boxed{994}$ .
$begin{align*} cot{alpha} + cot{beta} &= frac {cos{alpha}}{sin{alpha}} + frac {cos{beta}}{sin{beta}} = frac {sin{alpha}cos{beta} + cos{alpha}sin{beta}}{sin{alpha}sin{beta}} &= frac {sin{(alpha + beta)}}{sin{alpha}sin{beta}} = frac {sin{gamma}}{sin{alpha}sin{beta}} end{align*}$

By the Law of Cosines,

$[a^2 + b^2 - 2abcos{gamma} = c^2 = 1989c^2 - 2abcos{gamma} implies abcos{gamma} = 994c^2]$

Now

$begin{align*}frac {cot{gamma}}{cot{alpha} + cot{beta}} &= frac {cot{gamma}sin{alpha}sin{beta}}{sin{gamma}} = frac {cos{gamma}sin{alpha}sin{beta}}{sin^2{gamma}} = frac {ab}{c^2}cos{gamma} = frac {ab}{c^2} cdot frac {994c^2}{ab} &= boxed{994}end{align*}$

Use Law of cosines to give us $c^2=a^2+b^2-2abcos(gamma)$ or therefore $cos(gamma)=frac{994c^2}{ab}$ . Next, we are going to put all the sin's in term of $sin(a)$ . We get $sin(gamma)=frac{csin(a)}{a}$ . Therefore, we get $cot(gamma)=frac{994c}{bsin a}$ .

Next, use Law of Cosines to give us $b^2=a^2+c^2-2accos(beta)$ . Therefore, $cos(beta)=frac{a^2-994c^2}{ac}$ . Also, $sin(beta)=frac{bsin(a)}{a}$ . Hence, $cot(beta)=frac{a^2-994c^2}{bcsin(a)}$ .

Lastly, $cos(alpha)=frac{b^2-994c^2}{bc}$ . Therefore, we get $cot(alpha)=frac{b^2-994c^2}{bcsin(a)}$ .

Now, $frac{cot(gamma)}{cot(beta)+cot(alpha)}=frac{frac{994c}{bsin a}}{frac{a^2-994c^2+b^2-994c^2}{bcsin(a)}}$ . After using $a^2+b^2=1989c^2$ , we get $frac{994c*bcsin a}{c^2bsin a}=boxed{994}$ .

Let $gamma$ be $(180-alpha-beta)$

$frac{cot gamma}{cot alpha+cot beta} = frac{frac{-tan alpha tan beta}{tan(alpha+beta)}}{tan alpha + tan beta} = frac{(tan alpha tan beta)^2-tan alpha tan beta}{tan^2 alpha + 2tan alpha tan beta +tan^2 beta}$

WLOG, assume that $a$ and $c$ are legs of right triangle $abc$ with $beta = 90^o$ and $c=1$

By Pythagorean theorem, we have $b^2=a^2+1$ , and the given $a^2+b^2=1989$ . Solving the equations gives us $a=sqrt{994}$ and $b=sqrt{995}$ . We see that $tan beta = infty$ , and $tan alpha = sqrt{994}$ .

We see that our derived equation equals to $tan^2 alpha$ as $tan beta$ approaches infinity. Evaluating $tan^2 alpha$ , we get $boxed{994}$ .
Let the mode be $x$ , which we let appear $n > 1$ times. We let the arithmetic mean be $M$ , and the sum of the numbers $neq x$ be $S$ . Then $begin{align*} D &= left|M-xright| = left|frac{S+xn}{121}-xright| = left|frac{S}{121}-left(frac{121-n}{121}right)xright| end{align*}$ As $S$ is essentially independent of $x$ , it follows that we wish to minimize or maximize $x$ (in other words, $x=1,1000$ ). Indeed, $D(x)$ is symmetric about $x = 500.5$ ; consider replacing all of numbers $x_i$ in the sample with $1001-x_i$ , and the value of $D$ remains the same. So, without loss of generality, let $x=1$ . Now, we would like to maximize the quantity $frac{S}{121}-left(frac{121-n}{121}right)(1) = frac{S+n}{121}-1$ $S$ contains $121-n$ numbers that may appear at most $n-1$ times. Therefore, to maximize $S$ , we would have $1000$ appear $n-1$ times, $999$ appear $n-1$ times, and so forth. We can thereby represent $S$ as the sum of $n-1$ arithmetic series of $1000, 999, ldots, 1001 - leftlfloor frac{121-n}{n-1} rightrfloor$ . We let $k = leftlfloor frac{121-n}{n-1} rightrfloor$ , so $S = (n-1)left[frac{k(1000 + 1001 - k)}{2}right] + R(n)$ where $R(n)$ denotes the sum of the remaining $121-(n-1)k$ numbers, namely $R(n) = (121-(n-1)k)(1000-k)$ .At this point, we introduce the crude estimate^[1] that $k=frac{121-n}{n-1}$ , so $R(n) = 0$ and $begin{align*}2S+2n &= (121-n)left(2001-frac{121-n}{n-1}right)+2n = (120-(n-1))left(2002-frac{120}{n-1}right)end{align*}$ Expanding (ignoring the constants, as these do not affect which $n$ yields a maximum) and scaling, we wish to minimize the expression $5(n-1) + frac{36}{n-1}$ . By AM-GM, we have $5(n-1) + frac{36}{n-1} ge 2sqrt{5(n-1) cdot frac{36}{n-1}}$ , with equality coming when $5(n-1) = frac{36}{n-1}$ , so $n-1 approx 3$ . Substituting this result and some arithmetic gives an answer of $boxed{947}$ .
In less formal language, it quickly becomes clear after some trial and error that in our sample, there will be $n$ values equal to one and $n-1$ values each of $1000, 999, 998 ldots$ . It is fairly easy to find the maximum. Try $n=2$ , which yields $924$ , $n=3$ , which yields $942$ , $n=4$ , which yields $947$ , and $n=5$ , which yields $944$ . The maximum difference occurred at $n=4$ , so the answer is $947$ .
Call the midpoint of $overline{AB}$ $M$ and the midpoint of $overline{CD}$ $N$ . $d$ is the median of triangle $triangle CDM$ . The formula for the length of a median is $m=sqrt{frac{2a^2+2b^2-c^2}{4}}$ , where $a$ , $b$ , and $c$ are the side lengths of triangle, and $c$ is the side that is bisected by median $m$ . The formula is a direct result of the Law of Cosines applied twice with the angles formed by the median (Stewart's Theorem). We can also get this formula from the parallelogram law, that the sum of the squares of the diagonals is equal to the squares of the sides of a parallelogram (https://en.wikipedia.org/wiki/Parallelogram_law).We first find $CM$ , which is the median of $triangle CAB$ . $[CM=sqrt{frac{98+2592-1681}{4}}=frac{sqrt{1009}}{2}]$ Now we must find $DM$ , which is the median of $triangle DAB$ . $[DM=frac{sqrt{425}}{2}]$ Now that we know the sides of $triangle CDM$ , we proceed to find the length of $d$ .
$[d=frac{sqrt{548}}{2} Longrightarrow d^2=frac{548}{4}=boxed{137}]$
We first show that we can choose at most 5 numbers from ${1, 2, ldots , 11}$ such that no two numbers have a difference of $4$ or $7$ . We take the smallest number to be $1$ , which rules out $5,8$ . Now we can take at most one from each of the pairs: $[2,9]$ , $[3,7]$ , $[4,11]$ , $[6,10]$ . Now, $1989 = 180cdot 11 + 9$ . Because this isn't an exact multiple of $11$ , we need to consider some numbers separately.Notice that $1969 = 180cdot11 - 11 = 179cdot11$ . Therefore we can put the last $1969$ numbers into groups of 11. Now let's examine ${1, 2, ldots , 20}$ . If we pick $1, 3, 4, 6, 9$ from the first $11$ numbers, then we're allowed to pick $11 + 1$ , $11 + 3$ , $11 + 4$ , $11 + 6$ , $11 + 9$ . This means we get 10 members from the 20 numbers. Our answer is thus $179cdot 5 + 10 = boxed{905}$ .
First, we find the first three powers of :So we need to solve the diophantine equation .The minimum the left hand side can go is -54, so , so we try cases:
- Case 1: $a_3=2$
The only solution to that is $(a_1, a_2, a_3)=(2,9,2)$ .
- Case 2: $a_3=1$
The only solution to that is $(a_1, a_2, a_3)=(4,5,1)$ .
- Case 3: $a_3=0$
$a_3$ cannot be 0, or else we do not have a four digit number.

So we have the four digit integers $(292a_0)_{-3+i}$ and $(154a_0)_{-3+i}$ , and we need to find the sum of all integers $k$ that can be expressed by one of those.

$(292a_0)_{-3+i}$ :

We plug the first three digits into base 10 to get $30+a_0$ . The sum of the integers $k$ in that form is $345$ .

$(154a_0)_{-3+i}$ :

We plug the first three digits into base 10 to get $10+a_0$ . The sum of the integers $k$ in that form is $145$ . The answer is $345+145=boxed{490}$ .
Because we're given three concurrent cevians and their lengths, it seems very tempting to apply Mass points. We immediately see that $w_E = 3$ , $w_B = 1$ , and $w_A = w_D = 2$ . Now, we recall that the masses on the three sides of the triangle must be balanced out, so $w_C = 1$ and $w_F = 3$ . Thus, $CP = 15$ and $PF = 5$ .Recalling that $w_C = w_B = 1$ , we see that $DC = DB$ and $DP$ is a median to $BC$ in $triangle BCP$ . Applying Stewart's Theorem, $BC^2 + 12^2 = 2(15^2 + 9^2)$ , and $BC = 6sqrt {13}$ . Now notice that $2[BCP] = [ABC]$ , because both triangles share the same base and the $h_{triangle ABC} = 2h_{triangle BCP}$ . Applying Heron's formula on triangle $BCP$ with sides $15$ , $9$ , and $6sqrt{13}$ , $[BCP] = 54$ and $[ABC] = boxed{108}$ .Using a different form of Ceva's Theorem, we have $frac {y}{x + y} + frac {6}{6 + 6} + frac {3}{3 + 9} = 1Longleftrightarrowfrac {y}{x + y} = frac {1}{4}$ Solving $4y = x + y$ and $x + y = 20$ , we obtain $x = CP = 15$ and $y = FP = 5$ .Let $Q$ be the point on $AB$ such that $FC parallel QD$ . Since $AP = PD$ and $FPparallel QD$ , $QD = 2FP = 10$ . (Stewart's Theorem)Also, since $FCparallel QD$ and $QD = frac{FC}{2}$ , we see that $FQ = QB$ , $BD = DC$ , etc. (Stewart's Theorem) Similarly, we have $PR = RB$ ( $= frac12PB = 7.5$ ) and thus $RD = frac12PC = 4.5$ .
$PDR$ is a $3-4-5$ right triangle, so $angle PDR$ ( $angle ADQ$ ) is $90^circ$ . Therefore, the area of $triangle ADQ = frac12cdot 12cdot 6 = 36$ . Using area ratio, $triangle ABC = triangle ADBtimes 2 = left(triangle ADQtimes frac32right)times 2 = 36cdot 3 = boxed{108}$ .