- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2005AIME I真题及答案解析
2005AIME I真题及答案解析
答案解析请参考文末
Problem 1
Six congruent circles form a ring with each circle externally tangent to two circles adjacent to it. All circles are internally tangent to a circle ![]() with radius 30. Let
with radius 30. Let ![]() be the area of the region inside circle
be the area of the region inside circle ![]() and outside of the six circles in the ring. Find
and outside of the six circles in the ring. Find ![]()
Problem 2
For each positive integer ![]() let
let ![]() denote the increasing arithmetic sequence of integers whose first term is 1 and whose common difference is
denote the increasing arithmetic sequence of integers whose first term is 1 and whose common difference is ![]() For example,
For example, ![]() is the sequence
is the sequence ![]() For how many values of
For how many values of ![]() does
does ![]() contain the term 2005?
contain the term 2005?
Problem 3
How many positive integers have exactly three proper divisors (positive integral divisors excluding itself), each of which is less than 50?
Problem 4
The director of a marching band wishes to place the members into a formation that includes all of them and has no unfilled positions. If they are arranged in a square formation, there are 5 members left over. The director realizes that if he arranges the group in a formation with 7 more rows than columns, there are no members left over. Find the maximum number of members this band can have.
Problem 5
Robert has 4 indistinguishable gold coins and 4 indistinguishable silver coins. Each coin has an engraving of one face on one side, but not on the other. He wants to stack the eight coins on a table into a single stack so that no two adjacent coins are face to face. Find the number of possible distinguishable arrangements of the 8 coins.
Problem 6
Let ![]() be the product of the nonreal roots of
be the product of the nonreal roots of ![]() Find
Find ![]()
Problem 7
In quadrilateral ![]() and
and ![]() Given that
Given that ![]() where
where ![]() and
and ![]() are positive integers, find
are positive integers, find ![]()
Problem 8
The equation ![]() has three real roots. Given that their sum is
has three real roots. Given that their sum is ![]() where
where ![]() and
and ![]() are relatively prime positive integers, find
are relatively prime positive integers, find ![]()
Problem 9
Twenty-seven unit cubes are painted orange on a set of four faces so that the two unpainted faces share an edge. The 27 cubes are then randomly arranged to form a ![]() cube. Given that the probability that the entire surface of the larger cube is orange is
cube. Given that the probability that the entire surface of the larger cube is orange is ![]() where
where ![]() and
and ![]() are distinct primes and
are distinct primes and ![]() and
and ![]() are positive integers, find
are positive integers, find ![]()
Problem 10
Triangle ![]() lies in the Cartesian Plane and has an area of 70. The coordinates of
lies in the Cartesian Plane and has an area of 70. The coordinates of ![]() and
and ![]() are
are ![]() and
and ![]() respectively, and the coordinates of
respectively, and the coordinates of ![]() are
are ![]() The line containing the median to side
The line containing the median to side ![]() has slope
has slope ![]() Find the largest possible value of
Find the largest possible value of ![]()
Problem 11
A semicircle with diameter ![]() is contained in a square whose sides have length 8. Given the maximum value of
is contained in a square whose sides have length 8. Given the maximum value of ![]() is
is ![]() find
find ![]()
Problem 12
For positive integers ![]() let
let ![]() denote the number of positive integer divisors of
denote the number of positive integer divisors of ![]() including 1 and
including 1 and ![]() For example,
For example, ![]() and
and ![]() Define
Define ![]() by
by ![]() Let
Let ![]() denote the number of positive integers
denote the number of positive integers ![]() with
with ![]() odd, and let
odd, and let ![]() denote the number of positive integers
denote the number of positive integers ![]() with
with ![]() even. Find
even. Find ![]()
Problem 13
A particle moves in the Cartesian Plane according to the following rules:
- From any lattice point
 the particle may only move to
the particle may only move to  or
or 
- There are no right angle turns in the particle's path.
How many different paths can the particle take from ![]() to
to ![]() ?
?
Problem 14
Consider the points ![]() and
and ![]() There is a unique square
There is a unique square ![]() such that each of the four points is on a different side of
such that each of the four points is on a different side of ![]() Let
Let ![]() be the area of
be the area of ![]() Find the remainder when
Find the remainder when ![]() is divided by 1000.
is divided by 1000.
Problem 15
Triangle ![]() has
has ![]() The incircle of the triangle evenly trisects the median
The incircle of the triangle evenly trisects the median ![]() If the area of the triangle is
If the area of the triangle is ![]() where
where ![]() and
and ![]() are integers and
are integers and ![]() is not divisible by the square of a prime, find
is not divisible by the square of a prime, find ![]()
2005AIME I详细解析
- Define the radii of the six congruent circles as
 . If we draw all of the radii to the points of external tangency, we get a regular hexagon. If we connect the vertices of the hexagon to the center of the circle
. If we draw all of the radii to the points of external tangency, we get a regular hexagon. If we connect the vertices of the hexagon to the center of the circle  , we form several equilateral triangles. The length of each side of the triangle is
, we form several equilateral triangles. The length of each side of the triangle is  . Notice that the radius of circle
. Notice that the radius of circle  is equal to the length of the side of the triangle plus
is equal to the length of the side of the triangle plus  . Thus, the radius of
. Thus, the radius of  has a length of
has a length of  , and so
, and so  .
.  , so
, so  .
. - Suppose that the
 th term of the sequence
th term of the sequence  is
is  . Then
. Then  so
so  . The ordered pairs
. The ordered pairs  of positive integers that satisfy the last equation are
of positive integers that satisfy the last equation are  ,
, ,
,  ,
,  ,
,  ,
,  ,
,  ,
, ,
,  ,
,  ,
,  and
and  , and each of these gives a possible value of
, and each of these gives a possible value of  . Thus the requested number of values is
. Thus the requested number of values is  , and the answer is
, and the answer is  .Alternatively, notice that the formula for the number of divisors states that there are
.Alternatively, notice that the formula for the number of divisors states that there are  divisors of
divisors of  .
. - Suppose
 is such an integer. Then one of its factors is
is such an integer. Then one of its factors is  , so
, so  must be in the form
must be in the form  or
or  for distinct prime numbers
for distinct prime numbers  and
and  .In the first case, the three proper divisors of
.In the first case, the three proper divisors of  are
are  ,
,  and
and  . Thus, we need to pick two prime numbers less than
. Thus, we need to pick two prime numbers less than  . There are fifteen of these (
. There are fifteen of these ( and
and  ) so there are
) so there are  numbers of the first type.In the second case, the three proper divisors of
numbers of the first type.In the second case, the three proper divisors of  are 1,
are 1,  and
and  . Thus we need to pick a prime number whose square is less than
. Thus we need to pick a prime number whose square is less than  . There are four of these (
. There are four of these ( and
and  ) and so four numbers of the second type.Thus there are
) and so four numbers of the second type.Thus there are  integers that meet the given conditions.
integers that meet the given conditions. - If
 then
then  and so
and so  . If
. If  is an integer there are no numbers which are 5 more than a perfect square strictly between
is an integer there are no numbers which are 5 more than a perfect square strictly between  and
and  . Thus, if the number of columns is
. Thus, if the number of columns is  , the number of students is
, the number of students is  which must be 5 more than a perfect square, so
which must be 5 more than a perfect square, so  . In fact, when
. In fact, when  we have
we have  , so this number works and no larger number can. Thus, the answer is
, so this number works and no larger number can. Thus, the answer is  .
. - There are two separate parts to this problem: one is the color (gold vs silver), and the other is the orientation.There are
 ways to position the gold coins in the stack of 8 coins, which determines the positions of the silver coins.Create a string of letters H and T to denote the orientation of the top of the coin. To avoid making two faces touch, we cannot have the arrangement HT. Thus, all possible configurations must be a string of tails followed by a string of heads, since after the first H no more tails can appear. The first H can occur in a maximum of eight times different positions, and then there is also the possibility that it doesn’t occur at all, for
ways to position the gold coins in the stack of 8 coins, which determines the positions of the silver coins.Create a string of letters H and T to denote the orientation of the top of the coin. To avoid making two faces touch, we cannot have the arrangement HT. Thus, all possible configurations must be a string of tails followed by a string of heads, since after the first H no more tails can appear. The first H can occur in a maximum of eight times different positions, and then there is also the possibility that it doesn’t occur at all, for  total configurations. Thus, the answer is
total configurations. Thus, the answer is  .
. - The left-hand side of that equation is nearly equal to
 . Thus, we add 1 to each side in order to complete the fourth power and get
. Thus, we add 1 to each side in order to complete the fourth power and get  .Let
.Let ![$r = sqrt[4]{2006}$](https://latex.artofproblemsolving.com/6/e/a/6ea78ab025a46a9201473cb8c0fbbaca3b79df50.png) be the positive real fourth root of 2006. Then the roots of the above equation are
be the positive real fourth root of 2006. Then the roots of the above equation are  for
for  . The two non-real members of this set are
. The two non-real members of this set are  and
and  . Their product is
. Their product is  .
.  so
so  .
. - Draw the perpendiculars from
 and
and  to
to  , labeling the intersection points as
, labeling the intersection points as  and
and  . This forms 2
. This forms 2  right triangles, so
right triangles, so  and
and  . Also, if we draw the horizontal line extending from
. Also, if we draw the horizontal line extending from  to a point
to a point  on the line
on the line  , we find another right triangle
, we find another right triangle  .
.  . The Pythagorean Theorem yields that
. The Pythagorean Theorem yields that  , so
, so  . Therefore,
. Therefore,  , and
, and  .
. - Let
 . Then our equation reads
. Then our equation reads  or
or  . Thus, if this equation has roots
. Thus, if this equation has roots  and
and  , by Vieta's formulas we have
, by Vieta's formulas we have  . Let the corresponding values of
. Let the corresponding values of  be
be  and
and  . Then the previous statement says that
. Then the previous statement says that  so taking a logarithm of that gives
so taking a logarithm of that gives  and
and  . Thus the answer is
. Thus the answer is  .
. - The unit cube at the center of our large cube has no exterior faces, so all of its orientations work.For the six unit cubes and the centers of the faces of the large cube, we need that they show an orange face. This happens in
 of all orientations, so from these cubes we gain a factor of
of all orientations, so from these cubes we gain a factor of  .The twelve unit cubes along the edges of the large cube have two faces showing, and these two faces are joined along an edge. Thus, we need to know the number of such pairs that are both painted orange. We have a pair for each edge, and 7 edges border one of the unpainted faces while only 5 border two painted faces. Thus, the probability that two orange faces show for one of these cubes is
.The twelve unit cubes along the edges of the large cube have two faces showing, and these two faces are joined along an edge. Thus, we need to know the number of such pairs that are both painted orange. We have a pair for each edge, and 7 edges border one of the unpainted faces while only 5 border two painted faces. Thus, the probability that two orange faces show for one of these cubes is  , so from all of these cubes we gain a factor of
, so from all of these cubes we gain a factor of  .Finally, we need to orient the eight corner cubes. Each such cube has 3 faces showing, and these three faces share a common vertex. Thus, we need to know the number of vertices for which all three adjacent faces are painted orange. There are six vertices which are a vertex of one of the unpainted faces and two vertices which have our desired property, so each corner cube contributes a probability of
.Finally, we need to orient the eight corner cubes. Each such cube has 3 faces showing, and these three faces share a common vertex. Thus, we need to know the number of vertices for which all three adjacent faces are painted orange. There are six vertices which are a vertex of one of the unpainted faces and two vertices which have our desired property, so each corner cube contributes a probability of  and all the corner cubes together contribute a probability of
and all the corner cubes together contribute a probability of  Since these probabilities are independent, the overall probability is just their product,
Since these probabilities are independent, the overall probability is just their product,  and so the answer is
and so the answer is  .
. - The midpoint
 of line segment
of line segment  is
is  . The equation of the median can be found by
. The equation of the median can be found by  . Cross multiply and simplify to yield that
. Cross multiply and simplify to yield that  , so
, so  .Use determinants to find that the area of
.Use determinants to find that the area of  is
is  (note that there is a missing absolute value; we will assume that the other solution for the triangle will give a smaller value of
(note that there is a missing absolute value; we will assume that the other solution for the triangle will give a smaller value of  , which is provable by following these steps over again). We can calculate this determinant to become
, which is provable by following these steps over again). We can calculate this determinant to become 

 . Thus,
. Thus,  .Setting this equation equal to the equation of the median, we get that
.Setting this equation equal to the equation of the median, we get that  , so
, so  . Solving produces that
. Solving produces that  . Substituting backwards yields that
. Substituting backwards yields that  ; the solution is
; the solution is  .
. - We note that aligning the base of the semicircle with a side of the square is certainly non-optimal. If the semicircle is tangent to only one side of the square, we will have "wiggle-room" to increase its size. Once it is tangent to two adjacent sides of the square, we will maximize its size when it touches both other sides of the square. This can happen only when it is arranged so that the center of the semicircle lies on one diagonal of the square.
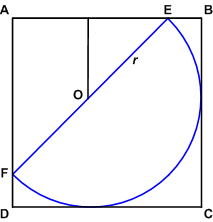 Now, let the square be
Now, let the square be  , and let
, and let  and
and  be the points at which the "corners" of the semicircle touch the square. Let
be the points at which the "corners" of the semicircle touch the square. Let  be the center of the semicircle.We can just look at a quarter circle inscribed in a
be the center of the semicircle.We can just look at a quarter circle inscribed in a  right triangle. We can then extend a radius,
right triangle. We can then extend a radius,  to one of the sides creating an
to one of the sides creating an  right triangle. This means that we have
right triangle. This means that we have  so
so  . Then the diameter is
. Then the diameter is  giving us
giving us 
- It is well-known that
 is odd if and only if
is odd if and only if  is a perfect square. (Otherwise, we can group divisors into pairs whose product is
is a perfect square. (Otherwise, we can group divisors into pairs whose product is  .) Thus,
.) Thus,  is odd if and only if there are an odd number of perfect squares less than
is odd if and only if there are an odd number of perfect squares less than  . So
. So  and
and  are odd, while
are odd, while  are even, and
are even, and  are odd, and so on.So, for a given
are odd, and so on.So, for a given  , if we choose the positive integer
, if we choose the positive integer  such that
such that  we see that
we see that  has the same parity as
has the same parity as  .It follows that the numbers between
.It follows that the numbers between  and
and  , between
, between  and
and  , and so on, all the way up to the numbers between
, and so on, all the way up to the numbers between  and
and  have
have  odd. These are the only such numbers less than
odd. These are the only such numbers less than  (because
(because  ).Notice that the difference between consecutive squares are consecutively increasing odd numbers. Thus, there are
).Notice that the difference between consecutive squares are consecutively increasing odd numbers. Thus, there are  numbers between
numbers between  (inclusive) and
(inclusive) and  (exclusive),
(exclusive),  numbers between
numbers between  and
and  , and so on. The number of numbers from
, and so on. The number of numbers from  to
to  is
is  . Whenever the lowest square beneath a number is odd, the parity will be odd, and the same for even. Thus,
. Whenever the lowest square beneath a number is odd, the parity will be odd, and the same for even. Thus, ![$a = [2(1) + 1] + [2(3) + 1] ldots [2(43) + 1] = 3 + 7 + 11 ldots 87$](https://latex.artofproblemsolving.com/8/b/d/8bdbe484939acf3d6a98aa3b93af6253a2fa1218.png) .
. ![$b = [2(2) + 1] + [2(4) + 1] ldots [2(42) + 1] + 70 = 5 + 9 ldots 85 + 70$](https://latex.artofproblemsolving.com/4/1/8/4184fc85b04350003e3c28ed8c3dcfca3ea4181c.png) , the
, the  accounting for the difference between
accounting for the difference between  and
and  , inclusive. Notice that if we align the two and subtract, we get that each difference is equal to
, inclusive. Notice that if we align the two and subtract, we get that each difference is equal to  . Thus, the solution is
. Thus, the solution is  .Similarly,
.Similarly,  , where the
, where the  accounts for those numbers between
accounts for those numbers between  and
and  .Thus
.Thus  .Then,
.Then,  . We can apply the formula
. We can apply the formula  . From this formula, it follows that
. From this formula, it follows that  and so that
and so that

 . Thus,
. Thus,
 .
. - The length of the path (the number of times the particle moves) can range from
 to
to  ; notice that
; notice that  gives the number of diagonals. Let
gives the number of diagonals. Let  represent a move to the right,
represent a move to the right,  represent a move upwards, and
represent a move upwards, and  to be a move that is diagonal. Casework upon the number of diagonal moves:
to be a move that is diagonal. Casework upon the number of diagonal moves:
- Case
 : It is easy to see only
: It is easy to see only  cases.
cases. - Case
 : There are two diagonals. We need to generate a string with
: There are two diagonals. We need to generate a string with 
 's,
's, 
 's, and
's, and 
 's such that no two
's such that no two  's or
's or  's are adjacent. The
's are adjacent. The  's split the string into three sections (
's split the string into three sections ( ): by the Pigeonhole principle all of at least one of the two letters must be all together (i.e., stay in a row).
): by the Pigeonhole principle all of at least one of the two letters must be all together (i.e., stay in a row).
- If both
 and
and  stay together, then there are
stay together, then there are  ways.
ways. - If either
 or
or  splits, then there are
splits, then there are  places to put the letter that splits, which has
places to put the letter that splits, which has  possibilities. The remaining letter must divide into
possibilities. The remaining letter must divide into  in one section and
in one section and  in the next, giving
in the next, giving  ways. This totals
ways. This totals  ways.
ways.
- Case
 : Now
: Now 
 's,
's, 
 's, and
's, and 
 's, so the string is divided into
's, so the string is divided into  partitions (
partitions ( ).
).
- If the
 's and
's and  's stay together, then there are
's stay together, then there are  places to put them.
places to put them. - If one of them splits and the other stays together, then there are
 places to put them, and
places to put them, and  ways to pick which splits, giving
ways to pick which splits, giving  ways.
ways. - If both groups split, then there are
 ways to arrange them. These add up to
ways to arrange them. These add up to  ways.
ways.
- Case
 : Now
: Now 
 ,
, 
 ,
, 
 's (
's ( ). There are
). There are  places to put
places to put  ,
,  places to put
places to put  , giving
, giving  ways.
ways. - Case
 : It is easy to see only
: It is easy to see only  case.
case.
Together, these add up to
 .
. - Case
- Consider a point
 such that
such that  is perpendicular to
is perpendicular to  ,
,  intersects
intersects  , and
, and  . E will be on the same side of the square as point
. E will be on the same side of the square as point  .Let the coordinates of
.Let the coordinates of  be
be  . Since
. Since  is perpendicular to
is perpendicular to  , and
, and  , we have
, we have  and
and  The coordinates of
The coordinates of  are thus
are thus  .Now, since
.Now, since  and
and  are on the same side, we find the slope of the sides going through
are on the same side, we find the slope of the sides going through  and
and  to be
to be  . Because the other two sides are perpendicular, the slope of the sides going through
. Because the other two sides are perpendicular, the slope of the sides going through  and
and  are now
are now  .Let
.Let  be the vertices of the square so that
be the vertices of the square so that  contains point
contains point  ,
,  contains point
contains point  , and etc. Since we know the slopes and a point on the line for each side of the square, we use the point slope formula to find the linear equations. Next, we use the equations to find
, and etc. Since we know the slopes and a point on the line for each side of the square, we use the point slope formula to find the linear equations. Next, we use the equations to find  vertices of the square, then apply the distance formula.We find the coordinates of
vertices of the square, then apply the distance formula.We find the coordinates of  to be
to be  and the coordinates of
and the coordinates of  to be
to be  . Applying the distance formula, the side length of our square is
. Applying the distance formula, the side length of our square is  .Hence, the area of the square is
.Hence, the area of the square is  . The remainder when
. The remainder when  is divided by
is divided by  is
is  .Let
.Let  denote a normal vector of the side containing
denote a normal vector of the side containing  . Note that
. Note that  intersect and hence must be opposite vertices of the square. The lines containing the sides of the square have the form
intersect and hence must be opposite vertices of the square. The lines containing the sides of the square have the form  ,
,  ,
,  , and
, and  . The lines form a square, so the distance between
. The lines form a square, so the distance between  and the line through
and the line through  equals the distance between
equals the distance between  and the line through
and the line through  , hence
, hence  , or
, or  . We can take
. We can take  and
and  . So the side of the square is
. So the side of the square is  , the area is
, the area is  , and the answer to the problem is
, and the answer to the problem is  .
. - Let
 ,
,  and
and  be the points of tangency of the incircle with
be the points of tangency of the incircle with  ,
,  and
and  , respectively. Without loss of generality, let
, respectively. Without loss of generality, let  , so that
, so that  is between
is between  and
and  . Let the length of the median be
. Let the length of the median be  . Then by two applications of the Power of a Point Theorem,
. Then by two applications of the Power of a Point Theorem,  , so
, so  . Now,
. Now,  and
and  are two tangents to a circle from the same point, so
are two tangents to a circle from the same point, so  and thus
and thus  . Then
. Then  so
so  and thus
and thus  .Now, by Stewart's Theorem in triangle
.Now, by Stewart's Theorem in triangle  with cevian
with cevian  , we have
, we have![[(3m)^2cdot 20 + 20cdot10cdot10 = 10^2cdot10 + (30 - 2c)^2cdot 10.]](https://latex.artofproblemsolving.com/a/2/4/a248c1a266345985cb02c044a0737792299201ce.png) Our earlier result from Power of a Point was that
Our earlier result from Power of a Point was that  , so we combine these two results to solve for
, so we combine these two results to solve for  and we get
and we get![[9(10 - c)^2 + 200 = 100 + (30 - 2c)^2 quad Longrightarrow quad c^2 - 12c + 20 = 0.]](https://latex.artofproblemsolving.com/b/1/e/b1e5c7de9eb4bc160b9bd0ac710cf4ef21a3de50.png) Thus
Thus  or
or  . We discard the value
. We discard the value  as extraneous (it gives us an equilateral triangle) and are left with
as extraneous (it gives us an equilateral triangle) and are left with  , so our triangle has area
, so our triangle has area  and so the answer is
and so the answer is  .Use Power of a point similar to the first solution to find that
.Use Power of a point similar to the first solution to find that  and that the side
and that the side  , where
, where  is one third of the median's length. Then use systems of law of cosines, creating two triangles, with
is one third of the median's length. Then use systems of law of cosines, creating two triangles, with  with angle
with angle  , and
, and  with the same angle. Solving the system yields
with the same angle. Solving the system yields  . Solving using Heron's Formula gets the answer
. Solving using Heron's Formula gets the answer  , or
, or  .
.
学术活动报名扫码了解!免费领取历年真题!
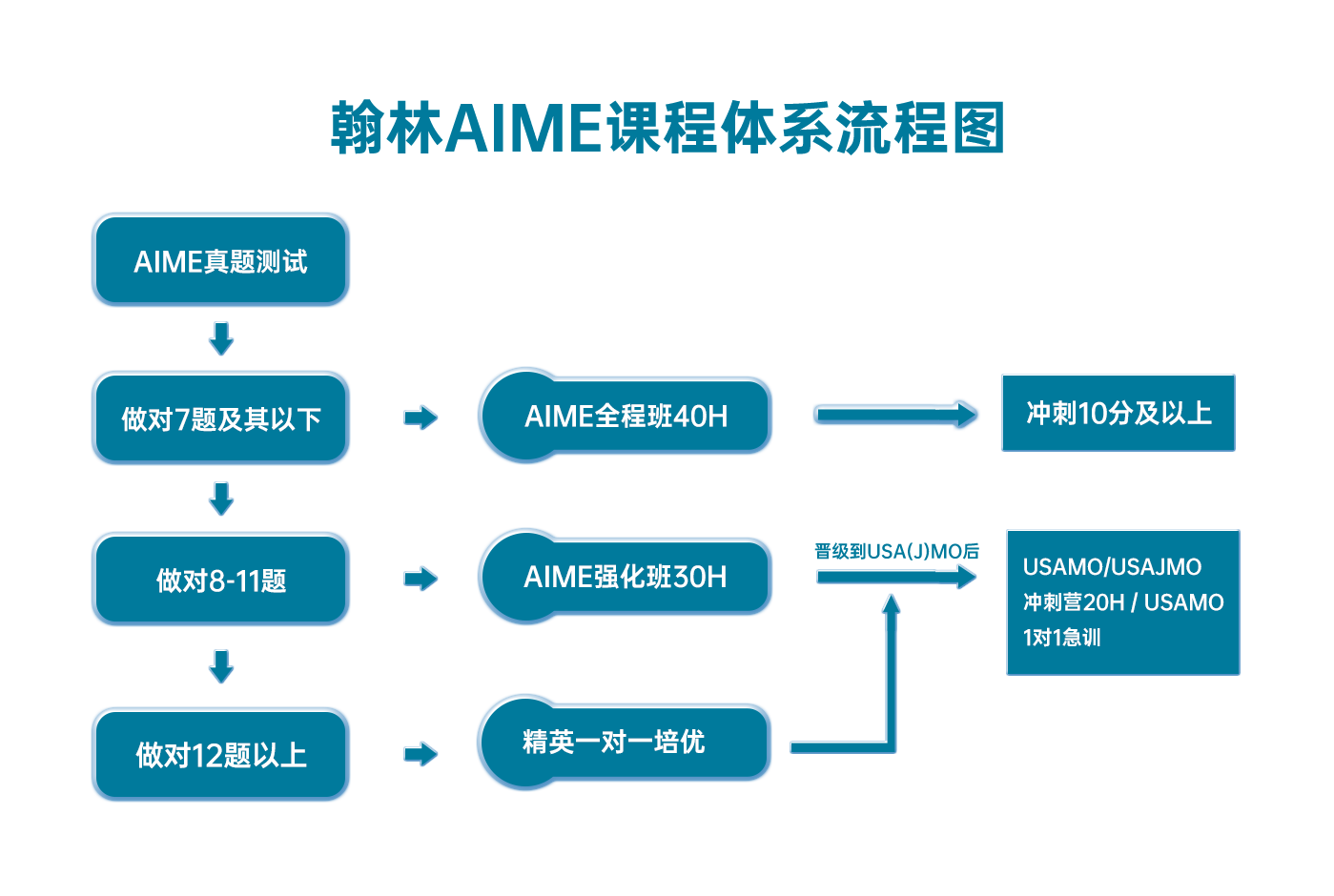
翰林AIME课程体系流程图

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









