- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2002 AMC12B 真题及答案详细解析
2002 AMC 12B 真题
答案详细解析请参考文末
Problem 1
The arithmetic mean of the nine numbers in the set ![]() is a
is a ![]() -digit number
-digit number ![]() , all of whose digits are distinct. The number
, all of whose digits are distinct. The number ![]() does not contain the digit
does not contain the digit
![]()
Problem 2
What is the value of![]()
when ![]() ?
?
![]()
Problem 3
For how many positive integers ![]() is
is ![]() a prime number?
a prime number?
![]()
Problem 4
Let ![]() be a positive integer such that
be a positive integer such that ![]() is an integer. Which of the following statements is not true:
is an integer. Which of the following statements is not true:
![]()
Problem 5
Let ![]() and
and ![]() be the degree measures of the five angles of a pentagon. Suppose that
be the degree measures of the five angles of a pentagon. Suppose that ![]() and
and ![]() and
and ![]() form an arithmetic sequence. Find the value of
form an arithmetic sequence. Find the value of ![]() .
.
![]()
Problem 6
Suppose that ![]() and
and ![]() are nonzero real numbers, and that the equation
are nonzero real numbers, and that the equation ![]() has solutions
has solutions ![]() and
and ![]() . Then the pair
. Then the pair ![]() is
is
![]()
Problem 7
The product of three consecutive positive integers is ![]() times their sum. What is the sum of their squares?
times their sum. What is the sum of their squares?
![]()
Problem 8
Suppose July of year ![]() has five Mondays. Which of the following must occur five times in August of year
has five Mondays. Which of the following must occur five times in August of year ![]() ? (Note: Both months have 31 days.)
? (Note: Both months have 31 days.)
![]()
Problem 9
If ![]() are positive real numbers such that
are positive real numbers such that ![]() form an increasing arithmetic sequence and
form an increasing arithmetic sequence and ![]() form a geometric sequence, then
form a geometric sequence, then ![]() is
is
![]()
Problem 10
How many different integers can be expressed as the sum of three distinct members of the set ![]() ?
?
![]()
Problem 11
The positive integers ![]() and
and ![]() are all prime numbers. The sum of these four primes is
are all prime numbers. The sum of these four primes is
![]()
Problem 12
For how many integers ![]() is
is ![]() the square of an integer?
the square of an integer?
![]()
Problem 13
The sum of ![]() consecutive positive integers is a perfect square. The smallest possible value of this sum is
consecutive positive integers is a perfect square. The smallest possible value of this sum is
![]()
Problem 14
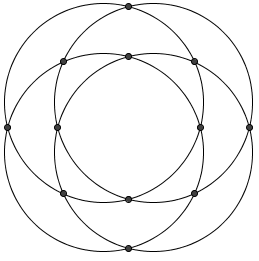
Four distinct circles are drawn in a plane. What is the maximum number of points where at least two of the circles intersect?
![]()
Problem 15
How many four-digit numbers ![]() have the property that the three-digit number obtained by removing the leftmost digit is one ninth of
have the property that the three-digit number obtained by removing the leftmost digit is one ninth of ![]() ?
?
![]()
Problem 16
Juan rolls a fair regular octahedral die marked with the numbers ![]() through
through ![]() . Then Amal rolls a fair six-sided die. What is the probability that the product of the two rolls is a multiple of 3?
. Then Amal rolls a fair six-sided die. What is the probability that the product of the two rolls is a multiple of 3?
![]()
Problem 17
Andy’s lawn has twice as much area as Beth’s lawn and three times as much area as Carlos’ lawn. Carlos’ lawn mower cuts half as fast as Beth’s mower and one third as fast as Andy’s mower. If they all start to mow their lawns at the same time, who will finish first?
![]()
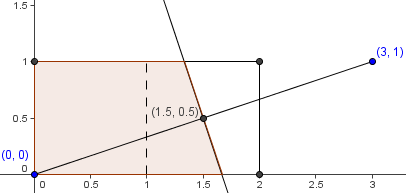
Problem 18
A point ![]() is randomly selected from the rectangular region with vertices
is randomly selected from the rectangular region with vertices ![]() . What is the probability that
. What is the probability that ![]() is closer to the origin than it is to the point
is closer to the origin than it is to the point ![]() ?
?
![]()
Problem 19
If ![]() and
and ![]() are positive real numbers such that
are positive real numbers such that ![]() and
and ![]() , then
, then ![]() is
is
![]()
Problem 20
Let ![]() be a right-angled triangle with
be a right-angled triangle with ![]() . Let
. Let ![]() and
and ![]() be the midpoints of legs
be the midpoints of legs ![]() and
and ![]() , respectively. Given that
, respectively. Given that ![]() and
and ![]() , find
, find ![]() .
.
![]()
Problem 21
For all positive integers ![]() less than
less than ![]() , let
, let

Calculate ![]() .
.
![]()
Problem 22
For all integers ![]() greater than
greater than ![]() , define
, define ![]() . Let
. Let ![]() and
and ![]() . Then
. Then ![]() equals
equals
![]()
Problem 23
In ![]() , we have
, we have ![]() and
and ![]() . Side
. Side ![]() and the median from
and the median from ![]() to
to ![]() have the same length. What is
have the same length. What is ![]() ?
?
![]()
Problem 24
A convex quadrilateral ![]() with area
with area ![]() contains a point
contains a point ![]() in its interior such that
in its interior such that ![]() . Find the perimeter of
. Find the perimeter of ![]() .
.
![]()
![]()
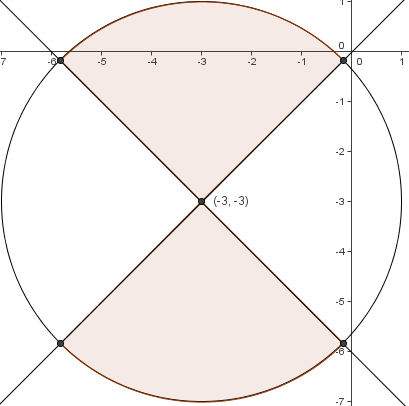
Problem 25
Let ![]() , and let
, and let ![]() denote the set of points
denote the set of points ![]() in the coordinate plane such that
in the coordinate plane such that![]() The area of
The area of ![]() is closest to
is closest to ![]()
2002 AMC12 B 真题答案详细解析
- Solution 1
We wish to find , or
, or  . This does not have the digit 0, so the answer is
. This does not have the digit 0, so the answer is  Solution 2
Solution 2
Notice that the final number is guaranteed to have the digits and that each of these digits can be paired with an even number adding up to 9.
and that each of these digits can be paired with an even number adding up to 9.  can be taken out, with the other digits fulfilling divisibility by 9.
can be taken out, with the other digits fulfilling divisibility by 9. - By the distributive property,
![$(3x-2)[(4x+1)-4x] + 1 = 3x-2 + 1 = 3x-1 = 3(4) - 1 = boxed{mathrm{(D)} 11}$](https://latex.artofproblemsolving.com/a/a/0/aa01f3de68b8e5cb8901b61622119f3327d4c7e0.png) .
. -
Solution 1
Factoring, we get
 . Either
. Either  or
or  is odd, and the other is even. Their product must yield an even number. The only prime that is even is
is odd, and the other is even. Their product must yield an even number. The only prime that is even is  , which is when
, which is when  is
is  . The answer is
. The answer is  .
.Solution 2
Considering parity, we see that
 is always even. The only even prime is
is always even. The only even prime is  , and so
, and so  whence
whence  .
. - Since
 ,
,![[0 < lim_{n rightarrow infty} left(frac{41}{42} + frac{1}{n}right) < frac {41}{42} + frac 1n < frac{41}{42} + frac 11 < 2]](https://latex.artofproblemsolving.com/0/a/1/0a117286e3f8f0f84a7cbc59b1204f101146fc51.png) From which it follows that
From which it follows that  and
and  . The only answer choice that is not true is
. The only answer choice that is not true is  .
. -
Solution 1
The sum of the degree measures of the angles of a pentagon (as a pentagon can be split into
 triangles) is
triangles) is  . If we let
. If we let  , it follows that
, it follows that![[(x-2d)+(x-d)+x+(x+d)+(x+2d) = 5x = 540 Longrightarrow x = 108 mathrm{(D)}]](https://latex.artofproblemsolving.com/2/a/0/2a03fa9f8fc2b8f56860f65f81e93bfc3b933f99.png)
Note that since
 is the middle term of an arithmetic sequence with an odd number of terms, it is simply the average of the sequence.
is the middle term of an arithmetic sequence with an odd number of terms, it is simply the average of the sequence.You can always assume the values are the same so

Solution 2
Let
 ,
,  ,
,  ,
,  ,
,  be
be  ,
,  ,
,  ,
,  ,
,  , respectively. Then we have
, respectively. Then we have![[v + w + x + y + z = 5v + 10d = 180^{circ} (5 - 2) = 540^{circ}]](https://latex.artofproblemsolving.com/b/3/9/b39bdd7d2dc26e54954af8dbd765bf22fb080ab0.png) Dividing the equation by
Dividing the equation by  , we have
, we have![[v + 2d = x = 108^{circ} mathrm {(D)}]](https://latex.artofproblemsolving.com/f/e/d/fedaf1b53101b80f4a59cff8d7b99979fd9bc9c5.png)
-
Solution 1
Since
 , it follows by comparing coefficients that
, it follows by comparing coefficients that  and that
and that  . Since
. Since  is nonzero,
is nonzero,  , and
, and  . Thus
. Thus  .
.Solution 2
Another method is to use Vieta's formulas. The sum of the solutions to this polynomial is equal to the opposite of the
 coefficient, since the leading coefficient is 1; in other words,
coefficient, since the leading coefficient is 1; in other words,  and the product of the solutions is equal to the constant term (i.e,
and the product of the solutions is equal to the constant term (i.e,  ). Since
). Since  is nonzero, it follows that
is nonzero, it follows that  and therefore (from the first equation),
and therefore (from the first equation),  . Hence,
. Hence, 
Solution 3 (Using the Answer Choices)
Note that for roots
 and
and  ,
,  . This implies that
. This implies that  is
is  , and there is only one answer choice with
, and there is only one answer choice with  in the position for
in the position for  , hence,
, hence, 
- Let the three consecutive positive integers be
 ,
,  , and
, and  . So,
. So,  .
.  , so
, so  . Hence, the sum of the squares is
. Hence, the sum of the squares is  .
. - If there are five Mondays, there are only three possibilities for their dates:
 ,
,  , and
, and  .In the first case August starts on a Thursday, and there are five Thursdays, Fridays, and Saturdays in August.In the second case August starts on a Wednesday, and there are five Wednesdays, Thursdays, and Fridays in August.In the third case August starts on a Tuesday, and there are five Tuesdays, Wednesdays, and Thursdays in August.The only day of the week that is guaranteed to appear five times is therefore
.In the first case August starts on a Thursday, and there are five Thursdays, Fridays, and Saturdays in August.In the second case August starts on a Wednesday, and there are five Wednesdays, Thursdays, and Fridays in August.In the third case August starts on a Tuesday, and there are five Tuesdays, Wednesdays, and Thursdays in August.The only day of the week that is guaranteed to appear five times is therefore  .
. -
Solution 1
We can let
 ,
,  ,
,  , and
, and  .
. 
Solution 2
As
 is a geometric sequence, let
is a geometric sequence, let  and
and  for some
for some  .
.Now,
 is an arithmetic sequence. Its difference is
is an arithmetic sequence. Its difference is  . Thus
. Thus 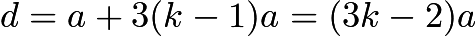 .
.Comparing the two expressions for
 we get
we get  . The positive solution is
. The positive solution is  , and
, and  .
.Solution 3
Letting
 be the common difference of the arithmetic progression, we have
be the common difference of the arithmetic progression, we have  ,
,  ,
,  . We are given that
. We are given that  =
=  , or
, or![[frac{a + n}{a} = frac{a + 3n}{a + n}.]](https://latex.artofproblemsolving.com/5/d/0/5d048c478d3ca0b242e47b5621c7d854827cbf34.png) Cross-multiplying, we get
Cross-multiplying, we get![[a^2 + 2an + n^2 = a^2 + 3an]](https://latex.artofproblemsolving.com/5/3/6/53646d5adaf792f94b95c1d9f0b0d4148a1b6a59.png)
![[n^2 = an]](https://latex.artofproblemsolving.com/5/6/4/5642d779ac0ea9621db97907b6908c51276813e5.png)
![[n = a]](https://latex.artofproblemsolving.com/f/0/3/f03bdc2df1bf326925e364582a4a26ca2c5483a0.png) So
So  .
. -
Solution 1
Subtracting 10 from each number in the set, and dividing the results by 3, we obtain the set
 . It is easy to see that we can get any integer between
. It is easy to see that we can get any integer between  and
and  inclusive as the sum of three elements from this set, for the total of
inclusive as the sum of three elements from this set, for the total of  integers.
integers.Solution 2
The set is an arithmetic sequence of numbers each
 more than a multiple of
more than a multiple of  . Thus the sum of any three numbers will be a multiple of
. Thus the sum of any three numbers will be a multiple of  . All the multiples of
. All the multiples of  from
from  to
to  are possible, totaling to
are possible, totaling to  integers.
integers. -
Solution1
Since
 and
and  must have the same parity, and since there is only one even prime number, it follows that
must have the same parity, and since there is only one even prime number, it follows that  and
and  are both odd. Thus one of
are both odd. Thus one of  is odd and the other even. Since
is odd and the other even. Since  , it follows that
, it follows that  (as a prime greater than
(as a prime greater than  ) is odd. Thus
) is odd. Thus  , and
, and  are consecutive odd primes. At least one of
are consecutive odd primes. At least one of  is divisible by
is divisible by  , from which it follows that
, from which it follows that  and
and  . The sum of these numbers is thus
. The sum of these numbers is thus  , a prime, so the answer is
, a prime, so the answer is  .
.Solution 2
In order for both
 and
and  to be prime, one of
to be prime, one of  must be 2, or else both
must be 2, or else both  ,
,  would be even numbers.
would be even numbers.If
 , then
, then  and
and  , which is not possible. Thus
, which is not possible. Thus  .
.Since
 is prime and
is prime and  , we can infer that
, we can infer that  and thus
and thus  can be expressed as
can be expressed as  for some natural number
for some natural number  .
.However in either case, one of
 and
and  can be expressed as
can be expressed as  which is a multiple of 3. Therefore the only possibility that works is when
which is a multiple of 3. Therefore the only possibility that works is when  and
and![[A + B + (A - B) + (A + B) = 5 + 2 + 3 + 7 = 17]](https://latex.artofproblemsolving.com/0/0/9/009d79e62fcb86d45c7d973d181b0c3b8d45bb69.png)
Which is a prime number.

-
Solution 1
Let
 , with
, with  (note that the solutions
(note that the solutions  do not give any additional solutions for
do not give any additional solutions for  ). Then rewriting,
). Then rewriting,  . Since
. Since  , it follows that
, it follows that  divides
divides  . Listing the factors of
. Listing the factors of  , we find that
, we find that  are the only
are the only  solutions (respectively yielding
solutions (respectively yielding  ).
).Solution 2
For
 and
and  the fraction is negative, for
the fraction is negative, for  it is not defined, and for
it is not defined, and for  it is between 0 and 1.
it is between 0 and 1.Thus we only need to examine
 and
and  .
.For
 and
and  we obviously get the squares
we obviously get the squares  and
and  respectively.
respectively.For prime
 the fraction will not be an integer, as the denominator will not contain the prime in the numerator.
the fraction will not be an integer, as the denominator will not contain the prime in the numerator.This leaves
 , and a quick substitution shows that out of these only
, and a quick substitution shows that out of these only  and
and  yield a square. Therefore, there are only
yield a square. Therefore, there are only  solutions (respectively yielding
solutions (respectively yielding  ).
).Solution 3
If
 , then
, then  and
and  , otherwise
, otherwise  will be negative. Thus
will be negative. Thus  and
and![[0 = frac{0}{20-(0)} le frac{n}{20-n} le frac{19}{20-(19)} = 19]](https://latex.artofproblemsolving.com/9/f/e/9feb430d115aea0e9e86b02cdd2ae225b49642b5.png) Checking all
Checking all  for which
for which  , we have
, we have  ,
,  ,
,  ,
,  as the possibilities.
as the possibilities. 
-
Solution 1
Let
 be the consecutive positive integers. Their sum,
be the consecutive positive integers. Their sum,  , is a perfect square. Since
, is a perfect square. Since  is a perfect square, it follows that
is a perfect square, it follows that  is a perfect square. The smallest possible such perfect square is
is a perfect square. The smallest possible such perfect square is  when
when  , and the sum is
, and the sum is  .
.Solution 2
Notice that all five choices given are perfect squares.
Let
 be the smallest number, we have
be the smallest number, we have![[a+(a+1)+(a+2)+...+(a+17)=18a+sum_{k=1}^{17}k=18a+153]](https://latex.artofproblemsolving.com/2/4/b/24ba9a08041a00d74638a06c236e5ee189a8420e.png)
Subtract
 from each of the choices and then check its divisibility by
from each of the choices and then check its divisibility by  , we have
, we have  as the smallest possible sum.
as the smallest possible sum. 
-
Solution 1
For any given pair of circles, they can intersect at most
 times. Since there are
times. Since there are  pairs of circles, the maximum number of possible intersections is
pairs of circles, the maximum number of possible intersections is  . We can construct such a situation as below, so the answer is
. We can construct such a situation as below, so the answer is  .
.Solution 2
Because a pair or circles can intersect at most
 times, the first circle can intersect the second at
times, the first circle can intersect the second at  points, the third can intersect the first two at
points, the third can intersect the first two at  points, and the fourth can intersect the first three at
points, and the fourth can intersect the first three at  points. This means that our answer is
points. This means that our answer is 
Solution 3
Pick a circle any circle-
 ways. Then, pick any other circle-
ways. Then, pick any other circle-  ways. For each of these circles, there will be
ways. For each of these circles, there will be  intersections for a total of
intersections for a total of  =
=  intersections. However, we have counted each intersection twice, so we divide for overcounting. Therefore, we reach a total of
intersections. However, we have counted each intersection twice, so we divide for overcounting. Therefore, we reach a total of  , which corresponds to
, which corresponds to  .
. -
Solution
Let
 , such that
, such that  . Then
. Then  . Since
. Since  , from
, from  we have
we have  three-digit solutions, and the answer is
three-digit solutions, and the answer is  .
.Solution 2
Since N is a four digit number, assume WLOG that
 , where a is the thousands digit, b is the hundreds digit, c is the tens digit, and d is the ones digit. Then,
, where a is the thousands digit, b is the hundreds digit, c is the tens digit, and d is the ones digit. Then,  , so
, so  Set these equal to each other:
Set these equal to each other:![[1000a + 100b + 10c + d = 900b + 90c + 9d]](https://latex.artofproblemsolving.com/b/7/2/b72664c9c2d440b53307369eea6d6aaa6ecec06b.png)
![[1000a = 800b + 80c + 8d]](https://latex.artofproblemsolving.com/f/2/f/f2f8a153a5faae42c32c8d0148d02754d6467809.png)
![[1000a = 8(100b + 10c + d)]](https://latex.artofproblemsolving.com/c/9/a/c9a42e8825cd2fc03cafaecc6ebbb3e5c13655bc.png) Notice that
Notice that  , thus:
, thus:![[1000a = 8(N - 1000a)]](https://latex.artofproblemsolving.com/5/a/6/5a6fd31a085282a10152f9253eb01d53febf2acf.png)
![[1000a = 8N - 8000a]](https://latex.artofproblemsolving.com/3/1/c/31c64a6abfacee012c060f51e9a642b78ce719e8.png)
![[9000a = 8N]](https://latex.artofproblemsolving.com/6/7/3/673099001a81a45b956ace6fd3d59d764495b69c.png)
![[N = 1125a]](https://latex.artofproblemsolving.com/f/b/5/fb5290b31d5c6fbc376e01e35889de01a86ccbae.png)
Go back to our first equation, in which we set
 , Then:
, Then:![[1125a = 1000a + 100b + 10c + d]](https://latex.artofproblemsolving.com/b/a/c/bacb4d586331e9c422106c7686f127b30f7b3fbc.png)
![[125a = 100b + 10c + d]](https://latex.artofproblemsolving.com/c/1/4/c149c7cf80e812d27d60a2b13b8ae3e6a26d7ab6.png) The upper limit for the right hand side (RHS) is
The upper limit for the right hand side (RHS) is  (when
(when  ,
,  , and
, and  ). It's easy to prove that for an
). It's easy to prove that for an  there is only one combination of
there is only one combination of  and
and  that can make the equation equal. Just think about the RHS as a three digit number
that can make the equation equal. Just think about the RHS as a three digit number  . There's one and only one way to create every three digit number with a certain combination of digits. Thus, we test for how many as are in the domain set by the RHS. Since
. There's one and only one way to create every three digit number with a certain combination of digits. Thus, we test for how many as are in the domain set by the RHS. Since  which is the largest
which is the largest  value, then
value, then  can be
can be  through
through  , giving us the answer of
, giving us the answer of 
-
Solution 1
On both dice, only the faces with the numbers
 are divisible by
are divisible by  . Let
. Let  be the probability that Juan rolls a
be the probability that Juan rolls a  or a
or a  , and
, and  that Amal does. By the Principle of Inclusion-Exclusion,
that Amal does. By the Principle of Inclusion-Exclusion,![[P(a cup b) = P(a) + P(b) - P(a cap b) = frac{1}{4} + frac{1}{3} - frac{1}{4} cdot frac{1}{3} = frac{1}{2} Rightarrow mathrm{(C)}]](https://latex.artofproblemsolving.com/c/c/2/cc29f83d1e2747949dccdb55b4eb258c113092a4.png)
Alternatively, the probability that Juan rolls a multiple of
 is
is  , and the probability that Juan does not roll a multiple of
, and the probability that Juan does not roll a multiple of  but Amal does is
but Amal does is  . Thus the total probability is
. Thus the total probability is  .
.Solution 2
The probability that neither Juan nor Amal rolls a multiple of
 is
is  ; using complementary counting, the probability that at least one does is
; using complementary counting, the probability that at least one does is  .
. - We say Andy's lawn has an area of
 . Beth's lawn thus has an area of
. Beth's lawn thus has an area of  , and Carlos's lawn has an area of
, and Carlos's lawn has an area of  .We say Andy's lawn mower cuts at a speed of
.We say Andy's lawn mower cuts at a speed of  . Carlos's cuts at a speed of
. Carlos's cuts at a speed of  , and Beth's cuts at a speed
, and Beth's cuts at a speed  .Each person's lawn is cut at a speed of
.Each person's lawn is cut at a speed of  , so Andy's is cut in
, so Andy's is cut in  time, as is Carlos's. Beth's is cut in
time, as is Carlos's. Beth's is cut in  , so the first one to finish is
, so the first one to finish is  .
. -
Solution 1
The region containing the points closer to
 than to
than to  is bounded by the perpendicular bisector of the segment with endpoints
is bounded by the perpendicular bisector of the segment with endpoints  . The perpendicular bisector passes through midpoint of
. The perpendicular bisector passes through midpoint of  , which is
, which is  , the center of the unit square with coordinates
, the center of the unit square with coordinates  . Thus, it cuts the unit square into two equal halves of area
. Thus, it cuts the unit square into two equal halves of area  . The total area of the rectangle is
. The total area of the rectangle is  , so the area closer to the origin than to
, so the area closer to the origin than to  and in the rectangle is
and in the rectangle is  . The probability is
. The probability is  .
.Solution 2
Assume that the point
 is randomly chosen within the rectangle with vertices
is randomly chosen within the rectangle with vertices  ,
,  ,
,  ,
,  . In this case, the region for
. In this case, the region for  to be closer to the origin than to point
to be closer to the origin than to point  occupies exactly
occupies exactly  of the area of the rectangle, or
of the area of the rectangle, or  square units.
square units.If
 is chosen within the square with vertices
is chosen within the square with vertices  ,
,  ,
,  ,
,  which has area
which has area  square unit, it is for sure closer to
square unit, it is for sure closer to  .
.Now if
 can only be chosen within the rectangle with vertices
can only be chosen within the rectangle with vertices  ,
,  ,
,  ,
,  , then the square region is removed and the area for
, then the square region is removed and the area for  to be closer to
to be closer to  is then decreased by
is then decreased by  square unit, left with only
square unit, left with only  square unit.
square unit.Thus the probability that
 is closer to
is closer to  is
is  and that of
and that of  is closer to the origin is
is closer to the origin is  .
. 
- Adding up the three equations gives
 . Subtracting each of the above equations from this yields, respectively,
. Subtracting each of the above equations from this yields, respectively,  . Taking their product,
. Taking their product,  .
. 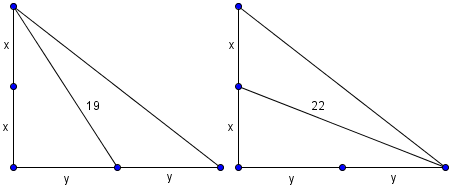 Let
Let  ,
,  . By the Pythagorean Theorem on
. By the Pythagorean Theorem on  respectively,
respectively, Summing these gives
Summing these gives  .By the Pythagorean Theorem again, we have
.By the Pythagorean Theorem again, we have![[(2x)^2 + (2y)^2 = XY^2 Longrightarrow XY = sqrt{4(x^2 + y^2)} = sqrt{4(169)} = sqrt{676} = boxed{mathrm{(B)} 26}]](https://latex.artofproblemsolving.com/f/1/6/f16445ea2f3d51273e055db6c290c3f43c9d12d2.png) Alternatively, we could note that since we found
Alternatively, we could note that since we found  , segment
, segment  . Right triangles
. Right triangles  and
and  are similar by Leg-Leg with a ratio of
are similar by Leg-Leg with a ratio of  , so
, so 
- Since
 , it follows that
, it follows that Thus
Thus  .
. - By the change of base formula,
 . Thus
. Thus
-
Solution 1
![[asy] unitsize(4cm); pair A, B, C, D, M; A = (1.768,0.935); B = (1.414,0); C = (0,0); D = (1.768,0); M = (0.707,0); draw(A--B--C--cycle); draw(A--D); draw(D--B); draw(A--M); label("$A$",A,N); label("$B$",B,S); label("$C$",C,S); label("$D$",D,S); label("$M$",M,S); label("$x$",(A+D)/2,E); label("$y$",(B+D)/2,S); label("$a$",(C+M)/2,S); label("$a$",(M+B)/2,S); label("$2a$",(A+M)/2,SE); label("$1$",(A+B)/2,SE); label("$2$",(A+C)/2,NW); draw(rightanglemark(B,D,A,3)); [/asy]](https://latex.artofproblemsolving.com/2/0/5/20552f4dac85af4806831750082aae9773f6b706.png)
Let
 be the foot of the altitude from
be the foot of the altitude from  to
to  extended past
extended past  . Let
. Let  and
and  . Using the Pythagorean Theorem, we obtain the equations
. Using the Pythagorean Theorem, we obtain the equations
Subtracting
 equation from
equation from  and
and  , we get
, we get
Then, subtracting
 from
from  and rearranging, we get
and rearranging, we get  , so
, so 
Solution 2
Let
 be the foot of the median from
be the foot of the median from  to
to  , and we let
, and we let  . Then by the Law of Cosines on
. Then by the Law of Cosines on  , we have
, we have
Since
 , we can add these two equations and get
, we can add these two equations and get![[5 = 10a^2]](https://latex.artofproblemsolving.com/b/7/e/b7ef5bf2a35df8f95e354145fc0ffc141e39ae7a.png)
Hence
 and
and  .
.Solution 3
From Stewart's Theorem, we have
 Simplifying, we get
Simplifying, we get 
- We have
![[[ABCD] = 2002 le frac 12 (AC cdot BD)]](https://latex.artofproblemsolving.com/6/8/4/68414870d9584f78410cfea4874a58e80bd8a5ce.png) (This is true for any convex quadrilateral: split the quadrilateral along
(This is true for any convex quadrilateral: split the quadrilateral along  and then using the triangle area formula to evaluate
and then using the triangle area formula to evaluate ![$[ACB]$](https://latex.artofproblemsolving.com/6/3/a/63a0c06761ee664f3ab0910bbf3336158cbf1645.png) and
and ![$[ACD]$](https://latex.artofproblemsolving.com/f/a/1/fa16d5df87a703864688635578a8f358b31ad6ef.png) ), with equality only if
), with equality only if  . By the triangle inequality,
. By the triangle inequality, with equality if
with equality if  lies on
lies on  and
and  respectively. Thus
respectively. Thus![[2002 le frac{1}{2} AC cdot BD le frac 12 cdot 52 cdot 77 = 2002]](https://latex.artofproblemsolving.com/7/6/3/763500d2bade003bb04e8fe0bcba8cc118de1a63.png) Since we have the equality case,
Since we have the equality case,  at point
at point  , as shown below.
, as shown below.![[asy] size(200); defaultpen(0.6); pair A = (0,0), B = (40,0), C = (25.6 * 52 / 24, 19.2 * 52 / 24), D = (40 - (40-25.6)*77/32,19.2*77/32), P = (25.6,19.2), Q = (25.6, 18.5); pair E=(A+P)/2, F=(B+P)/2, G=(C+P)/2, H=(D+P)/2; draw(A--B--C--D--cycle); draw(A--P--B--P--C--P--D); label("(A)",A,WSW); label("(B)",B,ESE); label("(C)",C,ESE); label("(D)",D,NW); label("(P)",Q,SSW); label("24",E,WNW); label("32",F,WSW); label("28",G,ESE); label("45",H,ENE); draw(rightanglemark(C,P,D,50)); [/asy]](https://latex.artofproblemsolving.com/b/e/0/be0cac31118507011fcd067dec64c89d4f9eee03.png)
 The perimeter of
The perimeter of  is
is  .
. - The first condition gives us that
![[x^2 + 6x + 1 + y^2 + 6y + 1 le 0 Longrightarrow (x+3)^2 + (y+3)^2 le 16]](https://latex.artofproblemsolving.com/b/b/8/bb8ffbea5beac4d271409e70b039ab3fd7fc571a.png) which is a circle centered at
which is a circle centered at  with radius
with radius  . The second condition gives us that
. The second condition gives us that![[x^2 + 6x + 1 - y^2 - 6y - 1 le 0 Longrightarrow (x^2 - y^2) + 6(x-y) le 0 Longrightarrow (x-y)(x+y+6) le 0]](https://latex.artofproblemsolving.com/d/c/f/dcfbc59e8ec63aca25e470670be7d5deb5925eca.png) Thus either
Thus either![[x - y ge 0,quad x+y+6 le 0]](https://latex.artofproblemsolving.com/e/6/5/e652e0c8f0c71d919631f0f09e73783e50ad2cae.png) or
or![[x - y le 0,quad x+y+6 ge 0]](https://latex.artofproblemsolving.com/e/e/2/ee27e9853791cc1fc519b576ce48f7f479902128.png)
Each of those lines passes through
 and has slope
and has slope  , as shown above. Therefore, the area of
, as shown above. Therefore, the area of  is half of the area of the circle, which is
is half of the area of the circle, which is  .
.
学术活动报名扫码了解!免费领取历年真题!

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1