Home » 国际竞赛 » 数学国际竞赛 » AMC美国数学竞赛 » Details

2007AMC10B真题与答案解析

Category: AMC美国数学竞赛, 国际竞赛 Date: 2019年12月4日下午5:54

2007AMC10B真题

答案解析请参考文末

Problem 1

Isabella's house has $3$ bedrooms. Each bedroom is $12$ feet long, $10$ feet wide, and $8$ feet high. Isabella must paint the walls of all the bedrooms. Doorways and windows, which will not be painted, occupy $60$ square feet in each bedroom. How many square feet of walls must be painted?

$textbf{(A) } 678 qquadtextbf{(B) } 768 qquadtextbf{(C) } 786 qquadtextbf{(D) } 867 qquadtextbf{(E) } 876$

Problem 2

Define the operation $star$ by $a star b = (a+b)b.$ What is $(3 star 5) - (5 star 3)?$

$textbf{(A) } -16 qquadtextbf{(B) } -8 qquadtextbf{(C) } 0 qquadtextbf{(D) } 8 qquadtextbf{(E) } 16$

Problem 3

A college student drove his compact car $120$ miles home for the weekend and averaged $30$ miles per gallon. On the return trip the student drove his parents' SUV and averaged only $20$ miles per gallon. What was the average gas mileage, in miles per gallon, for the round trip?

$textbf{(A) } 22 qquadtextbf{(B) } 24 qquadtextbf{(C) } 25 qquadtextbf{(D) } 26 qquadtextbf{(E) } 28$

Problem 4

The point $O$ is the center of the circle circumscribed about $triangle ABC,$ with $angle BOC=120^circ$ and $angle AOB=140^circ$ . What is the degree measure of $angle ABC?$

$textbf{(A) } 35 qquadtextbf{(B) } 40 qquadtextbf{(C) } 45 qquadtextbf{(D) } 50 qquadtextbf{(E) } 60$

Problem 5

In a certain land, all Arogs are Brafs, all Crups are Brafs, all Dramps are Arogs, and all Crups are Dramps. Which of the following statements is implied by these facts?

$textbf{(A) } text{All Dramps are Brafs and are Crups.}\ textbf{(B) } text{All Brafs are Crups and are Dramps.}\ textbf{(C) } text{All Arogs are Crups and are Dramps.}\ textbf{(D) } text{All Crups are Arogs and are Brafs.}\ textbf{(E) } text{All Arogs are Dramps and some Arogs may not be Crups.}$

Problem 6

The $2007$ $text{AMC}$ $10$ will be scored by awarding $6$ points for each correct response, $0$ points for each incorrect response, and $1.5$ points for each problem left unanswered. After looking over the $25$ problems, Sarah has decided to attempt the first $22$ and leave only the last $3$ unanswered. How many of the first $22$ problems must she solve correctly in order to score at least $100$ points?

$textbf{(A) } 13 qquadtextbf{(B) } 14 qquadtextbf{(C) } 15 qquadtextbf{(D) } 16 qquadtextbf{(E) } 17$

Problem 7

All sides of the convex pentagon $ABCDE$ are of equal length, and $angle A= angle B = 90^circ.$ What is the degree measure of $angle E?$

$textbf{(A) } 90 qquadtextbf{(B) } 108 qquadtextbf{(C) } 120 qquadtextbf{(D) } 144 qquadtextbf{(E) } 150$

Problem 8

On the trip home from the meeting where this AMC10 was constructed, the Contest Chair noted that his airport parking receipt had digits of the form $bbcac,$ where $0 le a < b < c le 9,$ and $b$ was the average of $a$ and $c.$ How many different five-digit numbers satisfy all these properties?

$textbf{(A) } 12 qquadtextbf{(B) } 16 qquadtextbf{(C) } 18 qquadtextbf{(D) } 20 qquadtextbf{(E) } 25$

Problem 9

A cryptographic code is designed as follows. The first time a letter appears in a given message it is replaced by the letter that is $1$ place to its right in the alphabet (assuming that the letter $A$ is one place to the right of the letter $Z$ ). The second time this same letter appears in the given message, it is replaced by the letter that is $1+2$ places to the right, the third time it is replaced by the letter that is $1+2+3$ places to the right, and so on. For example, with this code the word "banana" becomes "cbodqg". What letter will replace the last letter $s$ in the message $[text{"Lee's sis is a Mississippi miss, Chriss!"?}]$

$textbf{(A) } g qquadtextbf{(B) } h qquadtextbf{(C) } o qquadtextbf{(D) } s qquadtextbf{(E) } t$

Problem 10

Two points $B$ and $C$ are in a plane. Let $S$ be the set of all points $A$ in the plane for which $triangle ABC$ has area $1.$ Which of the following describes $S?$

$textbf{(A) } text{two parallel lines} qquadtextbf{(B) } text{a parabola} qquadtextbf{(C) } text{a circle} qquadtextbf{(D) } text{a line segment} qquadtextbf{(E) } text{two points}$

Problem 11

A circle passes through the three vertices of an isosceles triangle that has two sides of length $3$ and a base of length $2.$ What is the area of this circle?

$textbf{(A) } 2pi qquadtextbf{(B) } frac{5}{2}pi qquadtextbf{(C) } frac{81}{32}pi qquadtextbf{(D) } 3pi qquadtextbf{(E) } frac{7}{2}pi$

Problem 12

Tom's age is $T$ years, which is also the sum of the ages of his three children. His age $N$ years ago was twice the sum of their ages then. What is $T/N?$

$textbf{(A) } 2 qquadtextbf{(B) } 3 qquadtextbf{(C) } 4 qquadtextbf{(D) } 5 qquadtextbf{(E) } 6$

Problem 13

Two circles of radius $2$ are centered at $(2,0)$ and at $(0,2).$ What is the area of the intersection of the interiors of the two circles?

$textbf{(A) } pi -2 qquadtextbf{(B) } frac{pi}{2} qquadtextbf{(C) } frac{pi sqrt{3}}{3} qquadtextbf{(D) } 2(pi -2) qquadtextbf{(E) } pi$

Problem 14

Some boys and girls are having a car wash to raise money for a class trip to China. Initially $40%$ of the group are girls. Shortly thereafter two girls leave and two boys arrive, and then $30%$ of the group are girls. How many girls were initially in the group?

$textbf{(A) } 4 qquadtextbf{(B) } 6 qquadtextbf{(C) } 8 qquadtextbf{(D) } 10 qquadtextbf{(E) } 12$

Problem 15

The angles of quadrilateral $ABCD$ satisfy $angle A=2 angle B=3 angle C=4 angle D.$ What is the degree measure of $angle A,$ rounded to the nearest whole number?

$textbf{(A) } 125 qquadtextbf{(B) } 144 qquadtextbf{(C) } 153 qquadtextbf{(D) } 173 qquadtextbf{(E) } 180$

Problem 16

A teacher gave a test to a class in which $10%$ of the students are juniors and $90%$ are seniors. The average score on the test was $84.$ The juniors all received the same score, and the average score of the seniors was $83.$ What score did each of the juniors receive on the test?

$textbf{(A) } 85 qquadtextbf{(B) } 88 qquadtextbf{(C) } 93 qquadtextbf{(D) } 94 qquadtextbf{(E) } 98$

Problem 17

Point $P$ is inside equilateral $triangle ABC.$ Points $Q, R,$ and $S$ are the feet of the perpendiculars from $P$ to $overline{AB}, overline{BC},$ and $overline{CA},$ respectively. Given that $PQ=1, PR=2,$ and $PS=3,$ what is $AB?$

$textbf{(A) } 4 qquadtextbf{(B) } 3sqrt{3} qquadtextbf{(C) } 6 qquadtextbf{(D) } 4sqrt{3} qquadtextbf{(E) } 9$

Problem 18

A circle of radius $1$ is surrounded by $4$ circles of radius $r$ as shown. What is $r$ ?

$[asy] unitsize(3mm); defaultpen(linewidth(.8pt)+fontsize(7pt)); dotfactor=4; real r1=1, r2=1+sqrt(2); pair A=(0,0), B=(1+sqrt(2),1+sqrt(2)), C=(-1-sqrt(2),1+sqrt(2)), D=(-1-sqrt(2),-1-sqrt(2)), E=(1+sqrt(2),-1-sqrt(2)); pair A1=(1,0), B1=(2+2sqrt(2),1+sqrt(2)), C1=(0,1+sqrt(2)), D1=(0,-1-sqrt(2)), E1=(2+2sqrt(2),-1-sqrt(2)); path circleA=Circle(A,r1); path circleB=Circle(B,r2); path circleC=Circle(C,r2); path circleD=Circle(D,r2); path circleE=Circle(E,r2); draw(circleA); draw(circleB); draw(circleC); draw(circleD); draw(circleE); draw(A--A1); draw(B--B1); draw(C--C1); draw(D--D1); draw(E--E1); label("$1$",midpoint(A--A1),N); label("$r$",midpoint(B--B1),N); label("$r$",midpoint(C--C1),N); label("$r$",midpoint(D--D1),N); label("$r$",midpoint(E--E1),N); [/asy]$ $textbf{(A) } sqrt{2} qquadtextbf{(B) } 1+sqrt{2} qquadtextbf{(C) } sqrt{6} qquadtextbf{(D) } 3 qquadtextbf{(E) } 2+sqrt{2}$

Problem 19

The wheel shown is spun twice, and the randomly determined numbers opposite the pointer are recorded. The first number is divided by $4,$ and the second number is divided by $5.$ The first remainder designates a column, and the second remainder designates a row on the checkerboard shown. What is the probability that the pair of numbers designates a shaded square?

$[asy] unitsize(5mm); defaultpen(linewidth(.8pt)+fontsize(10pt)); dotfactor=4; real r=2; pair O=(0,0); pair A=(0,2), A1=(0,-2); draw(A--A1); pair B=(sqrt(3),1), B1=(-sqrt(3),-1); draw(B--B1); pair C=(sqrt(3),-1), C1=(-sqrt(3),1); draw(C--C1); path circleO=Circle(O,r); draw(circleO); pair[] ps={O}; dot(ps); label("$6$",(-0.6,1)); label("$1$",(0.6,1)); label("$2$",(0.6,-1)); label("$9$",(-0.6,-1)); label("$7$",(1.2,0)); label("$3$",(-1.2,0)); label("$pointer$",(-4,0)); draw((-5.5,0.5)--(-5.5,-0.5)--(-3,-0.5)--(-2.5,0)--(-3,0.5)--cycle); fill((4,0)--(4,1)--(5,1)--(5,0)--cycle,gray); fill((6,2)--(6,1)--(5,1)--(5,2)--cycle,gray); fill((6,0)--(6,-1)--(5,-1)--(5,0)--cycle,gray); fill((6,0)--(6,1)--(7,1)--(7,0)--cycle,gray); fill((4,-1)--(5,-1)--(5,-2)--(4,-2)--cycle,gray); fill((6,-1)--(7,-1)--(7,-2)--(6,-2)--cycle,gray); draw((4,2)--(7,2)--(7,-2)--(4,-2)--cycle); draw((4,1)--(7,1)); draw((4,0)--(7,0)); draw((4,-1)--(7,-1)); draw((5,2)--(5,-2)); draw((6,2)--(6,-2)); label("$1$",midpoint((4,-1)--(4,-2)),W); label("$2$",midpoint((4,0)--(4,-1)),W); label("$3$",midpoint((4,1)--(4,0)),W); label("$4$",midpoint((4,2)--(4,1)),W); label("$1$",midpoint((4,-2)--(5,-2)),S); label("$2$",midpoint((5,-2)--(6,-2)),S); label("$3$",midpoint((7,-2)--(6,-2)),S); [/asy]$ $textbf{(A) } frac{1}{3} qquadtextbf{(B) } frac{4}{9} qquadtextbf{(C) } frac{1}{2} qquadtextbf{(D) } frac{5}{9} qquadtextbf{(E) } frac{2}{3}$

Problem 20

A set of $25$ square blocks is arranged into a $5 times 5$ square. How many different combinations of $3$ blocks can be selected from that set so that no two are in the same row or column?

$textbf{(A) } 100 qquadtextbf{(B) } 125 qquadtextbf{(C) } 600 qquadtextbf{(D) } 2300 qquadtextbf{(E) } 3600$

Problem 21

Right $triangle ABC$ has $AB=3, BC=4,$ and $AC=5.$ Square $XYZW$ is inscribed in $triangle ABC$ with $X$ and $Y$ on $overline{AC}, W$ on $overline{AB},$ and $Z$ on $overline{BC}.$ What is the side length of the square?

$textbf{(A) } frac{3}{2} qquadtextbf{(B) } frac{60}{37} qquadtextbf{(C) } frac{12}{7} qquadtextbf{(D) } frac{23}{13} qquadtext{(E) 2}$

Problem 22

A player chooses one of the numbers $1$ through $4$ . After the choice has been made, two regular four-sided (tetrahedral) dice are rolled, with the sides of the dice numbered $1$ through $4.$ If the number chosen appears on the bottom of exactly one die after it has been rolled, then the player wins $1$ dollar. If the number chosen appears on the bottom of both of the dice, then the player wins $2$ dollars. If the number chosen does not appear on the bottom of either of the dice, the player loses $1$ dollar. What is the expected return to the player, in dollars, for one roll of the dice?

$textbf{(A) } -frac{1}{8} qquadtextbf{(B) } -frac{1}{16} qquadtextbf{(C) } 0 qquadtextbf{(D) } frac{1}{16} qquadtextbf{(E) } frac{1}{8}$

Problem 23

A pyramid with a square base is cut by a plane that is parallel to its base and $2$ units from the base. The surface area of the smaller pyramid that is cut from the top is half the surface area of the original pyramid. What is the altitude of the original pyramid?

$textbf{(A) } 2 qquadtextbf{(B) } 2+sqrt{2} qquadtextbf{(C) } 1+2sqrt{2} qquadtextbf{(D) } 4 qquadtextbf{(E) } 4+2sqrt{2}$

Problem 24

Let $n$ denote the smallest positive integer that is divisible by both $4$ and $9,$ and whose base- $10$ representation consists of only $4$ 's and $9$ 's, with at least one of each. What are the last four digits of $n?$

$textbf{(A) } 4444 qquadtextbf{(B) } 4494 qquadtextbf{(C) } 4944 qquadtextbf{(D) } 9444 qquadtextbf{(E) } 9944$

Problem 25

How many pairs of positive integers $(a,b)$ are there such that $a$ and $b$ have no common factors greater than $1$ and $[frac{a}{b} + frac{14b}{9a}]$ is an integer?

$textbf{(A) } 4 qquadtextbf{(B) } 6 qquadtextbf{(C) } 9 qquadtextbf{(D) } 12 qquadtextbf{(E) } text{infinitely many}$

2007AMC10B详细解析

There are four walls in each bedroom, since she can't paint floors or ceilings. So we calculate the number of square feet of wall there is in one bedroom: $[(12*8)+(12*8)+(10*8)+(10*8)-60=160+192-60=292]$ We have three bedrooms, so she must paint $[292*3=876 Rightarrow fbox{(E)}]$
Substitute and simplify. $[(3+5)5 - (5+3)3 = (3+5)2 = (8)2 = boxed{textbf{(E) }16}]$ Note that $(a star b) - (b star a) = (a+b)b - (b+a)a = (a+b)(b-a) = b^2 - a^2 = 5^2 - 3^2 = boxed{textbf{(E) }16}$ Note numbers were only plugged in at the end.
The trip was $240$ miles long and took $dfrac{120}{30}+dfrac{120}{20}=4+6=10$ gallons. Therefore, the average mileage was $dfrac{240}{10}= boxed{mathrm{(B) } 24}$ Alternatively, we can use the harmonic mean to get $frac{2}{frac{1}{20} + frac{1}{30}} = frac{2}{frac{1}{12}} = 24$ $longrightarrow boxed{textbf{(B)} }$
Because all the central angles of a circle add up to $360^circ,$ $begin{align*} angle BOC + angle AOB + angle AOC &= 360\ 120 + 140 + angle AOC &= 360\ angle AOC &= 100. end{align*}$ Therefore, the measure of $text{arc}AC$ is also $100^circ.$ Since the measure of an inscribed angle is equal to half the measure of the arc it intercepts, $angle ABC = boxed{textbf{(D)} 50}$
$[asy] unitsize(6mm); defaultpen(linewidth(.8pt)+fontsize(9pt)); dotfactor=4; real r1=1, r2=2, r3=3, r4=4; pair O1=(0,0), O2=(0,-0.5), O3=(0,-1), O4=(0,-1.5); path circleA=Circle(O1,r1); draw(circleA); path circleB=Circle(O2,r2); draw(circleB); path circleC=Circle(O3,r3); draw(circleC); path circleD=Circle(O4,r4); draw(circleD); label("$Crups$",(0,-.5)); label("$Dramps$",(0,-2)); label("$Arogs$",(0,-3.5)); label("$Brafs$",(0,-5)); [/asy]$ It may be easier to visualize this by drawing some sort of diagram. From the first statement, you can draw an Arog circle inside of the Braf circle, since all Arogs are Brafs, but not all Brafs are Arogs. Ignore the second statement for now, and draw a Dramp circle in the Arog circle and a Crup circle in the Dramp circle. You can see the second statement is already true because all Crups are Arogs. As you can see, the only statement that is true is $boxed{mathrm{(D)}}$
Sarah is leaving $3$ questions unanswered, guaranteeing her $3 times 1.5 = 4.5$ points. She will either get $6$ points or $0$ points for the rest of the questions. Let $x$ be the number of questions Sarah answers correctly. $begin{align*} 6x+4.5 &ge 100\ 6x &ge 95.5\ x &ge 15.92 end{align*}$ The number of questions she answers correctly has to be a whole number, so round up to get $boxed{textbf{(D) }16}$
$[asy] unitsize(1.5cm); defaultpen(linewidth(.8pt)+fontsize(10pt)); pair A=(0,2), B=(0,0), C=(2,0), D=(2+sqrt(3),1), E=(2,2); draw(A--B--C--D--E--cycle); draw(E--C,gray); draw(rightanglemark(B,A,E)); draw(rightanglemark(A,B,C)); label("$A$",A,NW); label("$B$",B,SW); label("$C$",C,SE); label("$D$",D,E); label("$E$",E,NE); [/asy]$ $AB = EC$ because they are opposite sides of a square. Also, $ED = DC = AB$ because all sides of the convex pentagon are of equal length. Since $ABCE$ is a square and $triangle CED$ is an equilateral triangle, $angle AEC = 90$ and $angle CED = 60.$ Use angle addition $[angle E = angle AEC + angle CED = 90 + 60 = boxed{textbf{(E)} 150}]$
For the average, $b,$ to be an integer, $a$ and $c$ have to either both be odd or both be even. There are $frac{5 times 4}{2 times 1} = 10$ ways to choose a set of two even numbers and $frac{5 times 4}{2 times 1} = 10$ ways to choose a set of two odd numbers. Therefore, the number of five-digit numbers that satisfy these properties is $10+10=boxed{textbf{(D) }20}$
Since the letter that will replace the last $s$ does not depend on any letter except the other $s$ 's, you can disregard anything else. There are $12$ $s$ 's, so the last $s$ will be replaced the letter $1+2+3+cdots+12$ places to the right of $s$ . $[1+2+3+cdots+12=12 times frac{1+12}{2} = 78]$ Every $26$ places, you will end up with the same letter so you can just take the remainder of $78$ when you divide by $26,$ which is $0.$ Therefore, the letter that will is replace the last $s$ is $boxed{textbf{(D) } s}$
Let $h$ be the length of the altitude of $triangle ABC.$ Since segment $BC$ is the base of the triangle and cannot change, the area of the triangle is $frac{1}{2}(BC)(h)=1$ and $h=frac{2}{BC}.$ Thus $S$ consists of two lines parallel to $BC$ and is $frac{2}{BC}$ units away from it. $longrightarrow boxed{mathrm{(A) } text{two parallel lines}}$
Solution 1

Let $triangle ABC$ have vertex $A$ and center $O$ , with foot of altitude from $A$ at $D$ .

$[asy] import olympiad; pair B=(0,0), C=(2,0), A=(1,3), D=(1,0); pair O=circumcenter(A,B,C); draw(A--B--C--A--D); draw(B--O--C); draw(circumcircle(A,B,C)); dot(O); label("(A)",A,N); label("(B)",B,S); label("(C)",C,S); label("(D)",D,S); label("(O)",O,W); label("(r)",(O+A)/2,SE); label("(r)",(O+B)/2,N); label("(h)",(O+D)/2,SE); label("(3)",(A+B)/2,NW); label("(1)",(B+D)/2,N); [/asy]$ Then by Pythagorean Theorem (with radius , height ) on

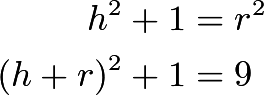
Substituting and solving gives $r = frac {9}{4sqrt {2}}$ . Then the area of the circle is $r^2 pi = left(frac {9}{4sqrt {2}}right)^2 pi = boxed{mathrm{(C) } frac {81}{32} pi}$ .

Solution 2

By $A = frac {1}{2}Bh = frac {abc}{4R}$ (or we could use $s = 4$ and Heron's formula), $[R = frac {abc}{2Bh} = frac {3 cdot 3 cdot 2}{2(2)(2sqrt {2})} = frac {9}{4sqrt {2}}]$ and the answer is $R^2 pi = boxed{mathrm{(C) } frac {81}{32} pi}$

Alternatively, by the Extended Law of Sines, $[2R = frac {AC}{sin angle ABC} = frac {3}{frac {2sqrt {2}}{3}} Longrightarrow R = frac {9}{4sqrt {2}}]$ Answer follows as above.

Solution 3

Extend segment $AD$ to $R$ on Circle $O$ .

$[asy] import olympiad; pair B=(0,0), C=(2,0), A=(1,3), D=(1,0), R=(1,-0.35); pair O=circumcenter(A,B,C); draw(A--B--C--A--D--R--C); draw(B--O--C); draw(circumcircle(A,B,C)); dot(O); label("(A)",A,N); label("(B)",B,S); label("(C)",C,S); label("(D)",D,S); label("(O)",O,W); label("(R)",R,S); label("(r)",(O+A)/2,SE); label("(r)",(O+R)/2,SE); label("(3)",(A+C)/2,NE); label("(1)",(C+D)/2,N); [/asy]$ By the Pythagorean Theorem

$triangle ADC$ is similar to $triangle ACR$ , so $[frac {2sqrt{2}}{3} = frac {3}{2r}]$ which gives us $[2r = frac {9}{2sqrt{2}} = frac {9sqrt{2}}{4}]$ therefore $[r = frac {9sqrt{2}}{8}]$

The area of the circle is therefore $pi r^2 = left(frac {9sqrt{2}}{8}right)^2 pi = boxed{mathrm{(C) } frac {81}{32} pi}$

Solution 4

First, we extend $AD$ to hit the circle at $E.$

$[asy] import olympiad; pair B=(0,0), C=(2,0), A=(1,3), D=(1,0), E=(1,-(8^0.5)/8); pair O=circumcenter(A,B,C); draw(A--B--C--A--E); draw(circumcircle(A,B,C)); dot(O); dot(D); dot(B); dot(C); dot(A); dot(E); label("$A$",A,N); label("$B$",B,S); label("(C)",C,S); label("$D$",D,NE); label("$O$",O,W); label("$E$",E,S); label("$3$",(A+B)/2,NW); label("$1$",(B+D)/2,N); [/asy]$ By the Pythagorean Theorem, we know thatWe also know that, from the Power of a Point Theorem,We can substitute the ones we know to getWe can simplify this to get thatWe add and together to get the length of the diameter, and then we can find the area.Therefore, the radius is , so the area is

Solution 5

Another possible solution is to plot the circle and triangle on a graph with the circle having center (0,0). Let the radius of the circle = $r$ . Let the distance between origin and base of triangle = $a$ .
```
 1 + a^2 = r^2 r + a = 2sqrt(2) a = (2)sqrt(2) - r 9 - (4r)sqrt(2) = 0 r = ((9)sqrt(2))/8 πr^2 = 81π/32
```
Tom's age $N$ years ago was $T-N$ . The ages of his three children $N$ years ago was $T-3N,$ since there are three people. If his age $N$ years ago was twice the sum of the children's ages then, $begin{align*}T-N&=2(T-3N)\ T-N&=2T-6N\ T&=5N\ T/N&=boxed{mathrm{(D) } 5}end{align*}$
You can find the area of half the intersection by subtracting the isosceles triangle in the sector from the whole sector. This sector is a quarter of the circle with radius $2,$ and the isosceles triangle is a right triangle. Therefore, the area of half the intersection is $[frac{1}{4} 4pi - frac{1}{2}(2)(2) = pi - 2]$ That means the area of the whole intersection is $boxed{mathrm{(D) } 2(pi-2)}$
If we let $p$ be the number of people initially in the group, the $0.4p$ is the number of girls. If two girls leave and two boys arrive, the number of people in the group is still $p,$ but the number of girls is $0.4p-2$ . Since only $30%$ of the group are girls, $begin{align*} frac{0.4p-2}{p}&=frac{3}{10}\ 4p-20&=3p\ p&=20end{align*}$ The number of girls is $0.4p=0.4(20)=boxed{mathrm{(C) } 8}$ There are the same number of total people before and after, but the number of girls has dropped by two and $10%$ . $frac{2}{0.1}=20$ , and $40%cdot20=8$ , so the answer is $mathrm{(C)}$ .
The sum of the interior angles of any quadrilateral is $360^circ.$ $begin{align*} 360 &= angle A + angle B + angle C + angle D\ &= angle A + frac{1}{2}A + frac{1}{3}A + frac{1}{4}A\ &= frac{12}{12}A + frac{6}{12}A + frac{4}{12}A + frac{3}{12}A\ &= frac{25}{12}A end{align*}$ $[angle A = 360 cdot frac{12}{25} = 172.8 approx boxed{mathrm{(D) } 173}]$
We can assume there are $10$ people in the class. Then there will be $1$ junior and $9$ seniors. The sum of everyone's scores is $10 cdot 84 = 840.$ Since the average score of the seniors was $83,$ the sum of all the senior's scores is $9 cdot 83 = 747.$ The only score that has not been added to that is the junior's score, which is $840 - 747 = boxed{mathrm{(C) } 93}$
Drawing $overline{PA}$ , $overline{PB}$ , and $overline{PC}$ , $triangle ABC$ is split into three smaller triangles. The altitudes of these triangles are given in the problem as $PQ$ , $PR$ , and $PS$ .Summing the areas of each of these triangles and equating it to the area of the entire triangle, we get: $[frac{s(1)}{2} + frac{s(2)}{2} + frac{s(3)}{2} = frac{s^2sqrt{3}}{4}]$ where $s$ is the length of a side $[s = boxed{mathrm{(D) } 4sqrt{3}}]$
Solution 1

You can express the line connecting the centers of an outer circle and the inner circle in two different ways. You can add the radius of both circles to get $r+1.$ You can also add the radius of two outer circles and use a $45-45-90$ triangle to get $frac{2r}{sqrt{2}} = rsqrt{2}.$ Since both representations are for the same thing, you can set them equal to each other. $begin{align*} r+1&=rsqrt{2}\ 1&=r(sqrt{2}-1)end{align*}$ $[r = frac{1}{sqrt{2}-1} = frac{1(sqrt{2}+1)}{(sqrt{2}-1)(sqrt{2}+1)} = frac{sqrt{2}+1}{2-1} = boxed{mathrm{(B) } 1 + sqrt{2}}]$

Solution 2

You can solve this problem by setting up a simple equation with the Pythagorean Theorem. The hypotenuse would be a segment that includes the radius of two circles on opposite corners and the diameter of the middle circle. This results in a segment of length $2r+2$ . The two legs are each the length between the centers of two large, adjacent circles, thus $2r$ . Using the Pythagorean Theorem: $begin{align*} (2r+2)^2 = 2(2r)^2\ 4r^2+8r+4=8r^2\ r^2+2r+1=2r^2\ r^2-2r-1=0\ r=frac{2+sqrt{4-(-4)}}{2}=frac{2+2sqrt{2}}{2}=boxed{mathrm{(B) } 1 + sqrt{2}} end{align*}$
Solution 1

When dividing each number on the wheel by $4,$ the remainders are $1, 1, 2, 2, 3,$ and $3.$ Each column on the checkerboard is equally likely to be chosen.

When dividing each number on the wheel by $5,$ the remainders are $1, 1, 2, 2, 3,$ and $4.$

The probability that a shaded square in the $1$ st or $3$ rd row of the $1$ st or $3$ rd column is chosen is $[frac{2}{3} times frac{3}{6} = frac{1}{3}]$

The probability that a shaded square in the $2$ nd or $4$ th row of the $2$ nd column is chosen is $[frac{1}{3} times frac{3}{6} = frac{1}{6}]$

Add those two together and you get $[frac{1}{3} + frac{1}{6} = frac{2}{6} + frac{1}{6} = frac{3}{6} = boxed{textbf{(C)} frac{1}{2}}]$

Solution 2

Alternatively, we may analyze this problem a little further.

First, we isolate the case where the rows are numbered 1 or 2. Notice that as listed before, the probability for picking a shaded square here is $[frac{1}{2}]$ because the column/row probabilities are the same, with the same number of shaded and non-shaded squares

Next we isolate the rows numbered 3 or 4. Note that the probability of picking the rows is same, because of our list up above. The columns, of course, still have the same probability. Because the number of shaded and non-shaded squares are equal, we have $[frac{1}{2}]$ Combining these we have a general probability of $[boxed{textbf{(C)} frac{1}{2}}]$
There are $25$ ways to choose the first square. The four remaining squares in its column and row, and the square you chose exclude nine squares from being chosen next time.There are $16$ remaining blocks to be chosen for the second square. The three remaining spaces in its row and column and the square you chose must be excluded from being chosen next time.Finally, the last square has $9$ remaining choices.The number of ways to choose $3$ squares is $25 cdot 16 cdot 9,$ but the order in which you chose the squares does not matter, so we divide by $3!$ . $[frac{25 cdot 16 cdot 9}{3 cdot 2 cdot 1} = 25 cdot 8 cdot 3 = 100 cdot 6 = boxed{mathrm{(C) } 600}]$

Solution 2

Once we choose our three squares, we will have occupied three separate columns $(A, B, C)$ and three separate rows. There are ${5 choose 3} times {5 choose 3}$ ways to choose these rows and columns.

There are $3$ ways to assign the square in column $A$ to a row, $2$ ways to assign the square in column $B$ to one of the remaining two rows, and poor square in column C doesn't get to choose. $:($

In total, we have $[{5 choose 3} times {5 choose 3} times 3!]$ which totals out to $boxed{mathrm{(C) } 600}$ .
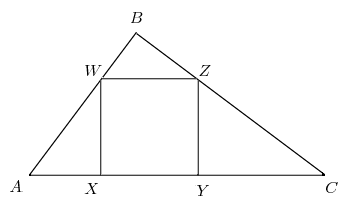
There are many similar triangles in the diagram, but we will only use $triangle WBZ sim triangle ABC.$ If $h$ is the altitude from $B$ to $AC$ and $s$ is the sidelength of the square, then $h-s$ is the altitude from $B$ to $WZ.$ By similar triangles, $begin{align*} frac{h-s}{s}&=frac{h}{5}\ 5h-5s&=hs\ 5h&=s(h+5)\ s&=frac{5h}{h+5} end{align*}$

Find the length of the altitude of $triangle ABC.$ Since it is a right triangle, the area of $triangle ABC$ is $frac{1}{2}(3)(4) = 6.$

The area can also be expressed as $frac{1}{2}(5)(h),$ so $frac{5}{2}h=6 longrightarrow h=2.4.$

Substitute back into $s.$

$[s=frac{5h}{h+5} = frac{12}{7.4} = boxed{mathrm{(B) } frac{60}{37}}]$

Let $l$ be the side length of the inscribed square. Note that $triangle ZYC sim triangle WBZ sim triangle ABC$ .

Then we can setup the following ratios:

$[frac{CZ}{l} = frac{5}{3} rightarrow CZ = frac{5}{3}l]$ $[frac{ZB}{l} = frac{4}{5} rightarrow ZB = frac{4}{5}l]$

But then $frac{5}{3}l+frac{4}{5}l = CZ+ZB = CB = 4 longrightarrow frac{37}{15}l=4 longrightarrow l = frac{60}{37} Longrightarrow boxed{mathrm{(B)}frac{60}{37}}$
There are $2 cdot 3 cdot 1 = 6$ ways for your number to show up once, $1 cdot 1 = 1$ way for your number to show up twice, and $3 cdot 3 = 9$ ways for your number to not show up at all. Think of this as a set of $16$ numbers with six $1s,$ one $2,$ and nine $-1s.$ The average of this set is the expected return to the player. $[frac{6(1)+1(2)-9(1)}{16} = frac{6+2-9}{16} = boxed{mathrm{(B) } -frac{1}{16}}]$
Since the two pyramids are similar, the ratio of the altitudes is the square root of the ratio of the surface areas.If $a$ is the altitude of the larger pyramid, then $a-2$ is the altitude of the smaller pyramid. $[frac{a}{a-2}=frac{sqrt{2}}{1} longrightarrow a= asqrt{2} - 2sqrt{2} longrightarrow asqrt{2}-a=2sqrt{2}]$ $[a=frac{2sqrt{2}}{sqrt{2}-1} = frac{4+2sqrt{2}}{2-1} = boxed{mathrm{(E) } 4+2sqrt{2}}]$
For a number to be divisible by $4,$ the last two digits have to be divisible by $4.$ That means the last two digits of this integer must be $4.$ For a number to be divisible by $9,$ the sum of all the digits must be divisible by $9.$ The only way to make this happen is with 9 $4$ 's. However, we also need one $9.$ The smallest integer that meets all these conditions is $4444444944$ . The last four digits are $boxed{mathrm{(C) } 4944}$
Solution 1

For reference, when given two numbers a and b, $a|b$ means that $b$ is divisible by $a$ *

Getting common denominators, we have to find coprime $(a,b)$ such that $9ab|9a^2+14b^2$ . b is divisible by 3 because 14 is not a multiple of three in the equation, so b must be so balance it and make them integers. Since $a$ and $b$ are coprime, $a|9a^2+14b^2 implies a|14$ . Similarly, $b|9$ . However, $b$ cannot be $9$ as $81a|81 cdot 14 + 9a^2$ only has solutions when $3|a$ . Therefore, $b=3$ and $a in {1,2,7,14}$ . Checking them all (Or noting that $4$ is the smallest answer choice), we see that they work and the answer is $boxed{mathrm{(A) } 4}$ .
- as per Wikipedia
Solution 2

Let $x = frac{a}{b}$ . We can then write the given expression as $x+frac{14}{9x} = k$ where $k$ is an integer. We can rewrite this as a quadratic, $9x^2 - 9kx + 14 = 0$ . By the Quadratic Formula, $x = frac{9kpmsqrt{81k^2-504}}{18} = frac{k}{2}pmfrac{sqrt{9k^2-56}}{6}$ . We know that $x$ must be rational, so $9k^2-56$ must be a perfect square. Let $9k^2-56 = n^2$ . Then, $56 = 9k^2-n^2 = (3k - n)(3k + n)$ . The factors pairs of $56$ are $1$ and $56$ , $2$ and $28$ , $4$ and $14$ , and $7$ and $8$ . Only $2$ and $28$ and $4$ and $14$ give integer solutions, $k = 5$ and $n = 13$ and $k = 3$ and $n = 5$ , respectively. Plugging these back into the original equation, we get $boxed{mathrm{(A) } 4}$ possibilities for $x$ , namely $frac{1}{3}, frac{14}{3}, frac{2}{3},$ and $frac{7}{3}$ .