翰林国际教育,国内国际竞赛领域的开拓者与引领者。我们不仅是系统辅导与深度教研的先行者,更为整个行业提供权威的赛事资讯与海量真题讲义。在数学、物理、化学、生物、计算机、商科、数模等核心领域,我们的战绩长期稳居头部领先地位,屡屡斩获国家队级别最高荣誉。作为同时拥有学科培训、AP国际学校及美高资质的权威教育组织,我们为学生提供一站式的卓越培养体系,助力英才迈向世界顶尖学府。
AMC10数学竞赛历年高频考点深度
一、 代数与函数:占比约35%
1. 方程与不等式
◦ 一次/二次方程:不仅是简单求解,更侧重含参方程的讨论(参数范围、根的性质判断)。例如,给定根的关系(如互为倒数、相反数)反推参数值。
◦ 高次方程:通过因式分解(分组、十字相乘)、代换法(如令 y = x + frac{1}{x} )降次求解。
◦ 不等式:重点是一元二次不等式、绝对值不等式的求解与几何意义(数轴上的距离)。常出现求整数解个数或解集范围的问题。
2. 函数与图像
◦ 函数性质:深入理解定义域、值域、单调性、奇偶性,并能从图像中读取信息。
◦ 函数变换:熟练掌握平移(“左加右减,上加下减”)、伸缩、对称等变换对解析式的影响。常考多种变换复合后的函数求值。
◦ 特殊函数:重点复习绝对值函数 f(x) = |ax+b| 和取整函数 f(x) = [x] 的图像、性质与方程求解。这类题综合性强,易设陷阱。
3. 数列与规律
◦ 等差数列/等比数列:熟练应用通项公式、求和公式,特别是等比数列求和公式 S_n = a_1 frac{1-r^n}{1-r} 。
◦ 递推数列:通过前几项找出规律,写出通项或求和。常与数论结合,要求写出某项的个位数字或余数。
二、 几何:占比约30%,直观与推理并重
几何题注重数形结合,既考查计算也考查逻辑证明,是区分度较高的模块。
1. 平面几何
◦ 三角形:相似三角形的判定与性质是重中之重,常与勾股定理、特殊角三角函数值(30°, 45°, 60°) 结合求边长。正弦定理、余弦定理也时有考查。
◦ 圆:必须熟练掌握圆幂定理(相交弦定理、切割线定理)、圆周角与圆心角关系。常见题型是求圆中线段长度或角度。
◦ 多边形与面积:常考正多边形、梯形、菱形等的性质。面积计算技巧包括割补法、等积变换。
2. 解析几何
◦ 直线与圆:求直线斜率、方程(点斜式)、两直线交点。求圆的方程、直线与圆的位置关系(相交、相切、相离)。
◦ 距离与面积:计算点与点、点与直线的距离。给定坐标求多边形面积(常用鞋带公式)。
3. 立体几何
◦ 主要考查长方体、正方体、圆柱、圆锥的基本性质,如求体积、表面积、空间两点最短路径(展开图)。
三、 数论:占比约15%,难度的体现
数论是AMC10的特色与难点,旨在选拔数学思维突出的学生,通常出现在中后部题目。
1. 整数的性质
◦ 整除特征:2, 3, 4, 5, 8, 9, 11等的快速判断法则必须熟记。常考“用数字组数”问题,如“用1-9各一次组成能被11整除的数”。
◦ 质数与合数:判断质数、分解质因数、求约数个数。关键定理:唯一分解定理。
◦ 奇偶性分析:利用奇偶性进行逻辑推理和排除选项,是解决数论和组合题的重要技巧。
2. 模运算与同余
◦ 这是数论难题的主要来源。理解模运算的基本性质(如 (a+b) mod m , (a times b) mod m )。
◦ 寻找周期规律:常要求计算 a^n mod m 的余数,通过寻找指数幂的个位数字或余数的循环周期来求解。
◦ 中国剩余定理:虽不直接考查定理本身,但考查其思想,即解方程组 x equiv a pmod{m}, x equiv b pmod{n} 。
四、 计数与概率:占比约20%
该模块考查逻辑的严谨性和思维的灵活性,是近年命题的热点。
1. 计数原理
◦ 排列与组合:这是绝对核心。必须准确区分“有序”(排列A)和“无序”(组合C)。常考分组问题、隔板法、圆排列、捆绑法与插空法。
◦ 容斥原理:用于解决重叠计数问题,如求两个或多个集合的并集元素个数。公式: |A cup B| = |A| + |B| - |A cap B| 。
2. 概率
◦ 古典概型: P = frac{text{满足条件的情况数}}{text{所有可能的情况数}} 。难点常在于准确计算出分子和分母。
◦ 几何概型:利用长度、面积或体积的比例来求概率。读题时需注意“均匀随机”等关键词。
◦ 条件概率与独立事件:理解概念,并能用乘法公式 P(AB) = P(A) cdot P(B|A) 计算。
五、 备考策略与高频考点融合
1. 专题突破与交叉融合
◦ 后期复习需重点关注代数与几何的结合(如建立坐标系解决几何问题)、数论与计数的结合(如求满足数论条件的数字个数)、概率与方程的结合
2. 真题导向与模拟训练
◦ 历年真题是最佳素材。通过精做真题,熟悉上述高频考点的出现形式、难度和陷阱设置方式。
◦ 进行限时模考,锻炼在75分钟内从前往后、先易后难的答题节奏,并实践“不会就空”的得分策略。
AMC10考前2个月高效冲刺策略
一、 精准诊断与针对性强化
最后两个月冲刺的核心在于精准定位薄弱环节并进行高强度专项突破,避免盲目刷题。
1. 知识图谱漏洞分析
◦ 通过近3年真题模拟测试,系统分析错题类型,建立个人知识薄弱点矩阵。重点区分知识性失分(公式不熟、概念混淆)、思维性失分(思路错误、无法建模)和心理性失分(粗心、时间分配不当)。
◦ 使用错题追踪系统,对常错知识点进行标记归类。例如:若在数论的同余问题连续出错,则需专项复习模运算性质、费马小定理应用等核心内容。
◦ 制定15日强化计划:前5日主攻代数与函数(含数列),中间5日突破几何与三角,后5日攻坚数论与组合概率,确保知识模块全覆盖。
2. 高频考点深度聚焦
◦ 代数:重点强化复杂因式分解技巧(分组、换元)、高次方程韦达定理应用、函数图像变换与性质综合题。
◦ 几何:专项训练圆幂定理与相似三角形的综合证明、立体几何空间思维题、解析几何快速计算技巧。
◦ 数论:熟练掌握整除特征快速判断法、同余方程解法、中国剩余定理的简化应用。
◦ 组合:加强复杂排列组合问题(捆绑法、插空法)、概率与统计结合题、图论基础问题的建模求解。
二、 真题实战与时间策略优化
冲刺阶段需通过高强度模拟训练提升应试能力,重点优化时间管理和答题策略。
1. 全真模拟考试环境
◦ 每周完成2-3套近年真题,严格遵循75分钟限时,使用答题卡填涂,完全模拟考场环境。
◦ 时间分段训练:
▪ 前30分钟:强制完成1-15题,训练基础题速答能力(平均2分钟/题)
▪ 中间30分钟:专注16-22题,提升中档题准确率(平均3-4分钟/题)
▪ 最后15分钟:攻坚23-25题+检查,培养难题抉择能力
◦ 建立时间预警机制:每10题设定完成时间节点(如30分钟时应完成前15题)
2. 智能答题策略应用
◦ 三遍答题法:
▪ 第一遍:快速解答确信会做的题目(目标20题)
▪ 第二遍:攻克有思路但需计算的题目(目标4题)
▪ 第三遍:专项突破难题或检查标记题
◦ 选择性放弃原则:对超过5分钟无思路的题目立即标记跳过,确保会做题目的得分率。利用"空题得1.5分"规则,规避盲目猜题风险。
◦ 答案验证技巧:培养代入检验、极端值验证、量纲分析等快速验算习惯,减少粗心失分。
三、 思维深化与创新解法训练
突破高分需要超越常规思维模式,培养解决新颖问题的能力。
1. 多解法思维拓展
◦ 对经典难题(如2021B卷25题)进行一题多解训练,比较代数法、几何法、数论法的效率差异。
◦ 开展命题逆向工程:针对典型结论反推条件设置,深度理解出题逻辑。
◦ 学习构造法证明:掌握反证法、数学归纳法等在组合、数论问题中的应用。
2. 创新题型应对策略
◦ 分析近3年新题型趋势:如跨模块综合题(数论+几何)、实际应用建模题(优化问题)、算法思维题(简单编程逻辑)。
◦ 建立问题拆解框架:面对复杂问题时,采用"条件梳理→知识定位→模型构建→分步解决"的标准化流程。
◦ 训练直觉猜想能力:通过特殊值检验、图形直观感知等方法快速探索解题方向。
四、 心理调整与临场发挥保障
最后阶段的准备需注重心理建设和考试当天的应对策略。
1. 压力适应训练
◦ 进行抗干扰模拟:在略有干扰的环境中进行模考,提升专注度。
◦ 建立积极心理暗示:制定分数目标区间(如100-115分),避免完美主义焦虑。
◦ 呼吸放松法练习:在遇到难题时进行30秒深呼吸调整,避免紧张情绪蔓延。
2. 临场应对方案
◦ 物资准备清单:提前准备准考证、身份证件、多个计算器、铅笔、手表等。
◦ 突发情况预案:如遇设备故障、临时不适等问题时的应对流程。
◦ 后程时间管理:最后15分钟必须预留5分钟检查时间,重点核对前15题的基础题答案。
◦ 交卷前最终检查:确认答题卡填涂无误、没有漏题,核对关键计算步骤。
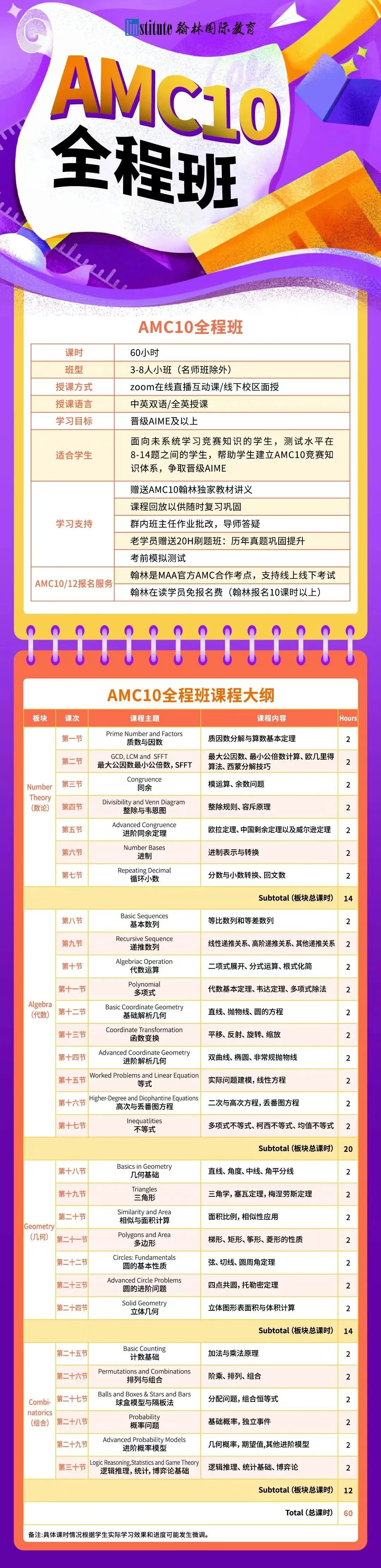
翰林AMC10培训班
翰林AMC10培训班