翰林国际教育,国内国际竞赛领域的开拓者与引领者。我们不仅是系统辅导与深度教研的先行者,更为整个行业提供权威的赛事资讯与海量真题讲义。在数学、物理、化学、生物、计算机、商科、数模等核心领域,我们的战绩长期稳居头部领先地位,屡屡斩获国家队级别最高荣誉。作为同时拥有学科培训、AP国际学校及美高资质的权威教育组织,我们为学生提供一站式的卓越培养体系,助力英才迈向世界顶尖学府。
一、参赛对象与年级定位
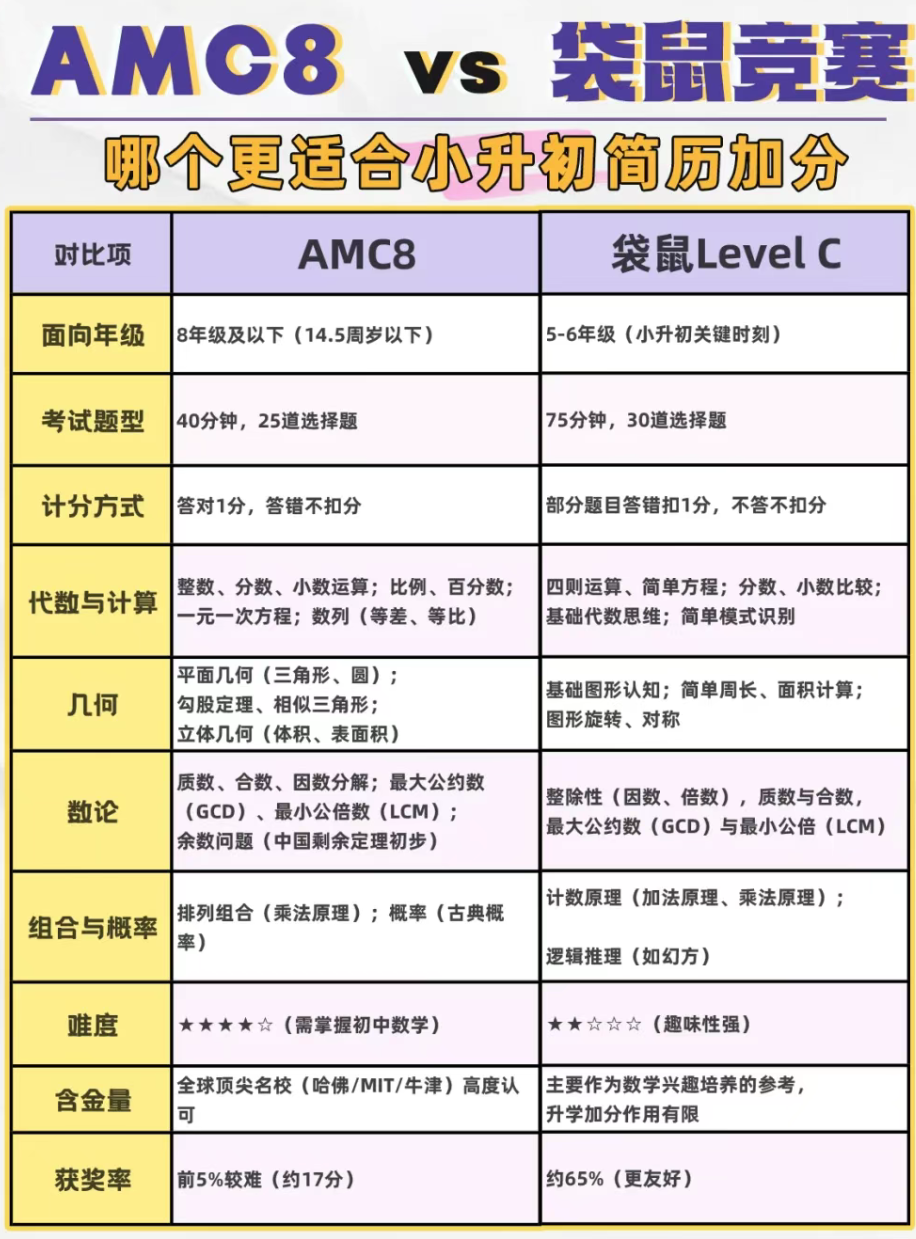
AMC8明确规定参赛者须为8年级及以下学生(年龄不超过14.5周岁),主要面向初中低年级和数学能力突出的高年级小学生。这项竞赛的设计初衷是为美国及全球优秀学生提供挑战平台,因此对参赛者的数学基础和能力要求较高。
袋鼠数学竞赛Level C的参赛对象主要为5-6年级学生,年龄层次明显低于AMC8。该竞赛采用分层设计,Level C专门针对小学高年级学生,注重激发数学兴趣和培养基础思维,参赛门槛相对较低,更适合数学学习时间较短但希望接触竞赛的学生。
二、考试形式与题型设计
AMC8采用高强度考试模式:40分钟内完成25道选择题,平均每道题仅1.6分钟解题时间。这种设置强调解题速度和熟练度,考验学生在压力下的应变能力。计分方式采用答对得1分,答错不扣分的规则,鼓励学生尝试解答所有题目。
袋鼠竞赛Level C的考试安排更为宽松:75分钟完成30道选择题,平均每道题有2.5分钟思考时间。其计分规则独具特色:部分题目采用答错扣1分、不答不扣分的机制,这种设计旨在培养学生谨慎答题的习惯,避免盲目猜测,同时保留适当的挑战性。
三、代数与计算能力要求
在代数与计算领域,AMC8的要求明显更高。参赛者需要掌握整数、分数、小数的综合运算能力,熟练运用比例和百分数解决实际问题,能够解一元一次方程并理解数列概念(包括等差数列和等比数列)。这些内容已经达到初中数学水平,需要较强的抽象思维能力。
袋鼠竞赛Level C的代数要求相对基础,主要考察四则运算能力、简单方程求解、分数与小数的比较和转换。虽然也涉及基础代数思维和模式识别,但更注重对数学概念的直观理解和基本应用,难度控制在小学阶段范围内。
四、几何知识体系对比
AMC8的几何部分要求系统掌握平面几何知识,包括三角形和圆的性质、勾股定理的应用、相似三角形的判定与性质,以及图形变换(旋转、对称)等进阶内容。这些知识点需要学生具备良好的空间想象能力和逻辑推理能力。
袋鼠竞赛Level C的几何内容以立体几何为主,重点考察长方体、正方体等基本几何体的体积和表面积计算,对平面几何的要求较低。这种设计更符合小学生的认知特点,通过具体实物帮助学生建立几何直观。
五、数论与组合概率深度
AMC8在数论方面要求较高,学生需要理解质数与合数的性质,掌握因数分解技巧,熟练运用最大公约数(GCD)和最小公倍数(LCM)解决实际问题,甚至初步接触中国剩余定理等较深奥的内容。组合与概率部分要求掌握排列组合(乘法原理)和古典概率计算,这些内容都需要较强的逻辑思维能力。
袋鼠竞赛Level C在数论方面要求较低,主要考察基础计数原理(加法原理、乘法原理)和逻辑推理能力(如幻方问题)。这些内容更注重思维过程的训练,而非具体知识点的深度挖掘,适合数论基础较弱的学生。
六、难度等级与挑战性
AMC8的难度评级为四星(需掌握初中数学),相当于初中数学竞赛水平。竞赛题目往往需要多步推导和创造性思维,对学生的数学素养和解题技巧都有较高要求。前5%的获奖分数线通常约为17分(满分25),竞争激烈,获奖难度较大。
袋鼠竞赛Level C的难度评级为三星(趣味性强),题目设计更注重趣味性和启发性。竞赛通过图形、故事等生动形式呈现数学问题,降低了参与门槛。约65%的获奖率使更多学生能够获得成就感,有利于培养数学兴趣。
七、含金量与升学助力
AMC8被全球顶尖名校(如哈佛、MIT、牛津等)高度认可,成绩优异者甚至可能获得直接邀请参加更高级别竞赛(如AMC10/12)的机会。在小升初简历中,AMC8奖项能够显著体现学生的数学天赋和学术潜力,尤其受到优质民办初中和国际学校的重视。
袋鼠竞赛主要作为数学兴趣培养的参考,其升学加分作用相对有限。虽然获奖证书可作为学生参与国际活动的证明,但难以与AMC8的权威性相提并论。该竞赛更适合作为数学学习的补充和兴趣培养的途径。
八、备赛策略与选择建议
基于以上分析,两项竞赛的备赛策略应有明显区别:
对于AMC8,建议提前1-2年开始系统准备。首先要扎实掌握初中数学基础知识,然后进行专项训练,特别是数论和组合概率等难点领域。大量真题练习和模拟考试必不可少,同时要注重时间管理能力的培养。对于袋鼠竞赛,备赛重点应放在基础知识的巩固和解题技巧的训练上。由于竞赛趣味性强,可以通过游戏化学习方式培养兴趣。建议从4年级开始接触往届真题,逐步建立解题信心。
袋鼠竞赛衔接AMC8需补充知识点
数论部分
需掌握质数与合数的性质与判断方法,理解约数与倍数的关系,学习整除规则及余数问题的解法。这些内容是AMC8数论基础。
组合计数
在逻辑推理基础上,需补充排列组合的计算方法,掌握容斥原理的应用,熟练运用加法原理和乘法原理解决复杂计数问题。
几何提升
需加强空间想象能力,学习圆与扇形的周长面积计算,掌握勾股定理及其应用,理解三角形的基本性质。
解题策略
需要学习假设法、分组法等高级方法,掌握比例关系的复杂应用,熟练运用排除法、列表法和特殊值法等技巧。
计算能力
需强化分数、百分数、小数的混合运算,掌握新定义运算的解题方法,提升复杂计算题的准确性和效率。建议通过专项练习逐步掌握这些知识点,每周保持系统训练,才能顺利实现从袋鼠到AMC8的过渡。










