翰林国际教育,国内国际竞赛领域的开拓者与引领者。我们不仅是系统辅导与深度教研的先行者,更为整个行业提供权威的赛事资讯与海量真题讲义。在数学、物理、化学、生物、计算机、商科、数模等核心领域,我们的战绩长期稳居头部领先地位,屡屡斩获国家队级别最高荣誉。作为同时拥有学科培训、AP国际学校及美高资质的权威教育组织,我们为学生提供一站式的卓越培养体系,助力英才迈向世界顶尖学府。
AMC10竞赛知识点系统汇总
AMC10的知识体系可划分为四大核心模块:代数、几何、数论、组合。每个模块都包含了从基础到进阶的丰富内容。
1. 代数(Algebra)
- 侧重于函数、方程与技巧
● 代数是AMC10中占比最重、应用最广泛的模块,强调抽象思维和灵活变形。 多项式与方程 多项式运算: 多项式的加、减、乘、除,特别是多项式除法与长除法技巧。
○ 余数定理与因式定理: 多项式f(x)除以(x - a)的余数为f(a)。若f(a)=0,则(x - a)是f(x)的一个因式。这是求解高次方程根的关键。
○ 韦达定理及其推广: 对于二次方程ax²+bx+c=0,根与系数有关系:x₁+x₂ = -b/a, x₁x₂ = c/a。对于更高次方程,也存在对称多项式形式的根与系数关系。
○ 特殊高次方程: 可因式分解的高次方程、可通过换元法转化为二次方程的方程(如双二次方程)、以及一些特殊形式的方程。
● 不等式 均值不等式(AM-GM): 若干个非负数的算术平均数不小于其几何平均数,这是证明和求解最值问题的最强大工具之一。
○ 柯西-施瓦茨不等式、排序不等式等: 这些是不等式领域的进阶工具,常用于处理更复杂的最值问题。
○ 不等式求解: 涉及二次不等式、分式不等式及绝对值不等式。
● 函数 函数概念: 函数的定义、定义域和值域的确定(尤其注意分母、根号等限制条件)。
○ 具体函数类型: 二次函数: 顶点式、交点式、标准式之间的转换,图像性质(开口、对称轴、顶点、截距),最值问题。
■ 指数与对数函数: 运算法则,图像与性质,求解指数/对数方程。
■ 简单三角函数: 正弦、余弦、正切在直角三角形中的定义,特殊角函数值,正弦定理和余弦定理(虽属几何,但常与代数结合)。
● 数列 等差数列与等比数列: 通项公式,求和公式及其推导。
○ 递推数列: 通过递推关系定义数列,并求解其通项公式(如特征根法)。
○ 求和技巧: 裂项相消、错位相减法等。
● 代数技巧进阶 代数式恒等变形、配方、对称多项式、构造法、设而不求等高级解题策略。
2. 几何(Geometry)
- 侧重于图形性质与空间想象
● 几何模块要求考生具备敏锐的观察力和严谨的逻辑推理能力。 平面几何进阶 三角形: 重要定理: 正弦定理、余弦定理、角平分线定理、塞瓦定理、梅涅劳斯定理。
■ 心: 内心、外心、垂心、重心(统称“四心”)的性质及其坐标表示。
■ 特殊三角形: 等边、等腰、直角三角形的性质与判定。
○ 圆: 圆幂定理: 相交弦定理、切割线定理、割线定理的统一表述。
■ 圆与四边形: 圆内接四边形的判定与性质(对角互补、外角等于内对角),圆外切四边形的性质(对边之和相等)。
■ 四点共圆: 多种判定方法(如对角互补、同底同侧等角)。
○ 多边形: 正多边形的角度、边长、面积、外接圆与内切圆的关系。
○ 解析几何入门: 坐标系中点的距离、中点公式、直线方程(点斜式、两点式)、圆方程、直线与圆的位置关系。
● 立体几何 空间关系: 点、线、面的平行与垂直关系。
○ 三维坐标系: 空间点的坐标、距离公式。
○ 常见几何体: 多面体: 棱柱、棱锥(特别是正棱锥)的体积与表面积计算。
■ 旋转体: 圆柱、圆锥、球的体积与表面积公式。
○ 欧拉公式: 对于凸多面体,顶点数(V) - 棱数(E) + 面数(F) = 2。
3. 数论(Number Theory)
- 侧重于整数的精妙性质
● 数论是AMC10的特色和难点,考察思维的严谨性与创造性。 整数性质 整除性: 整除规则(如被2, 3, 4, 5, 8, 9, 11等数整除的判定),带余除法。
○ 质数与合数: 质数判定、质数分布、分解质因数。
○ 因数与倍数: 最大公约数(GCD)、最小公倍数(LCM)的求法(辗转相除法)及应用。
○ 奇偶性分析: 利用奇偶性进行逻辑推理和排除选项。
● 模运算 同余概念与基本性质: a ≡ b (mod m) 的含义,同余式的加、减、乘运算。
○ 复杂同余问题: 求大数的余数、利用同余解决整数分类问题、费马小定理的初步应用。
● 进制 不同进制(如二进制、五进制、十六进制)与十进制之间的相互转换,以及在特定进制下的运算。
● 丢番图方程 主要是一次和二次不定方程,特别是勾股数组、佩尔方程等特殊形式的求解。
4. 组合(Combinatorics)
- 侧重于计数与策略
● 组合数学是衡量数学思维灵活性的重要标尺。 计数原理 加法原理与乘法原理: 所有计数问题的基础,必须准确理解“分类”与“分步”的区别。
○ 排列与组合: 区分是否与顺序有关,熟练掌握P(n, r)和C(n, r)公式及适用场景。
○ 容斥原理: 解决重叠计数问题,公式:|A∪B| = |A| + |B| - |A∩B|,并可推广至三个及以上集合。
● 二项式定理 公式:(a+b)^n = Σ [C(n, k) * a^(n-k) * b^k]。熟悉其通项公式及系数性质(如对称性、各项系数和)。
● 概率 古典概型: 概率 P = 满足条件的情况数 / 所有可能的情况数。
○ 几何概型: 利用长度、面积或体积的比例来计算概率。
○ 期望值: 离散随机变量的期望值计算,即每个结果的值乘以其概率再求和。
● 组合方法进阶 递推: 建立计数问题的递推关系式(如斐波那契数列)并求解。
○ 对应原理: 通过建立一一映射将复杂计数问题转化为简单问题(如“隔板法”解决不定方程非负整数解问题)。
○ 分类讨论: 对复杂问题根据特定标准进行不重不漏的分类。
○ 图论与游戏问题: 简单的图论概念(如点、边、路径)、对策问题等。
AMC10高频知识点考察分析
在四大模块中,考察频率和比重并非均等。根据历年真题统计,其分布呈现出显著规律:
● 代数与几何占据绝对主导(合计超60%): 这两部分是数学的基础支柱,是考查学生数学核心能力的主要阵地。代数更偏重计算与变形,几何更偏重推理与洞察。
● 数论比重稳步提升: 因其能很好区分顶尖学生,数论题目的数量和难度近年来有所增加,成为高分的关键突破口。
● 组合是最大变数: 组合题目灵活多变,是主要难点和区分点。掌握基本原理后,更需要临场的创造性思维。
各模块内最常出现的具体考点包括:
● 代数模块: 基础运算与应用题: 比例、百分比、行程问题、工作效率问题等,难点在于准确理解题意并建立数学模型。
○ 多项式: 利用余数定理/因式定理求根或参数。
○ 数列: 等差数列与等比数列的求和问题,以及简单的递推数列。
● 几何模块: 三角形计算: 综合运用勾股定理、相似、正弦/余弦定理求边长或面积。
○ 圆的性质: 利用圆幂定理和四点共圆解决线段长度问题。
○ 面积计算: 图形的割补法、等积变形。
● 数论模块: 质因数分解: 求一个数的约数个数、约数和,或解决与乘积、整除相关的问题。
○ 模运算: 求大数除以某数的余数,或利用奇偶性、模分析解决整数存在性问题。
● 组合模块: 基本计数: 熟练运用排列组合、乘法原理解决受限的计数问题(如“不相邻”用插空法)。
○ 概率计算: 古典概型是绝对主流,关键是准确计数。
AMC10高频易错点深度解析
许多学生知识点已掌握,却在考试中失分,根源往往在于以下易错点:
1. 代数(Algebra)易错点
● 应用题审题不清: 未能捕捉关键信息(如“至少”、“至多”、“翻倍”、“提前”),或忽略单位换算(小时/分钟、米/厘米)。
● 绝对值与根式处理不当: 求解含绝对值方程或不等式时,忽略正负讨论;处理根式时忽略定义域(被开方数非负)。
● 指数/对数运算性质混淆: 尤其是log(a+b) ≠ log a + log b这类错误。
● 韦达定理应用错误: 在使用x₁² + x₂² = (x₁+x₂)² - 2x₁x₂等变形时,忘记系数a的影响。
2. 几何(Geometry)易错点
● “想当然”的几何直观: 仅凭图形外观作出判断,忽视严格证明。例如,看似垂直的角未必是90度,看似相等的线段未必相等。
● 全等/相似三角形判定错误: 未能准确找到对应角或对应边,尤其是在复杂图形中。
● 漏解或多解: 几何问题经常存在多种情况(如高在三角形内部或外部、圆与圆的位置关系),考生因思维定式而漏解。
● 解析几何计算失误: 距离公式、中点公式等计算繁琐,容易在正负号上出错。
3. 计数(Counting)易错点
● 排列与组合混淆: 无法判断问题是否与顺序有关。例如,“选派代表”是组合,“排成一排”是排列。
● 重复计数: 这是组合计数中最常见的错误。在使用乘法原理或分类讨论时,方案之间并非完全独立,导致某些情况被多次计算。
● 遗漏计数: 与重复计数相反,分类标准不清晰,导致某些合法情况被忽略。
● 隔板法应用条件不清: 隔板法(Sticks and Bars)要求分配对象是 相同的 ,且用于解决“每份至少一个”的问题。若条件变化(如允许为0),需进行转化。
4. 数论(Number Theory)易错点
● 质数概念模糊: 误认为1是质数,或忘记2是唯一的偶质数。
● 模运算性质错误: 错误地认为除法也满足同余性(即a ≡ b (mod m) 不能直接推出a/c ≡ b/c (mod m))。
● 枚举不完整: 在解决整数解问题时,枚举所有可能情况时发生遗漏。
5. 概率(Probability)易错点
● 基本事件空间定义错误: 未能确保所有基本事件是等可能的。
● 条件概率理解偏差: 混淆P(A|B)和P(B|A)。
● 几何概型度量错误: 在计算几何概率时,对长度、面积或体积的度量计算错误。
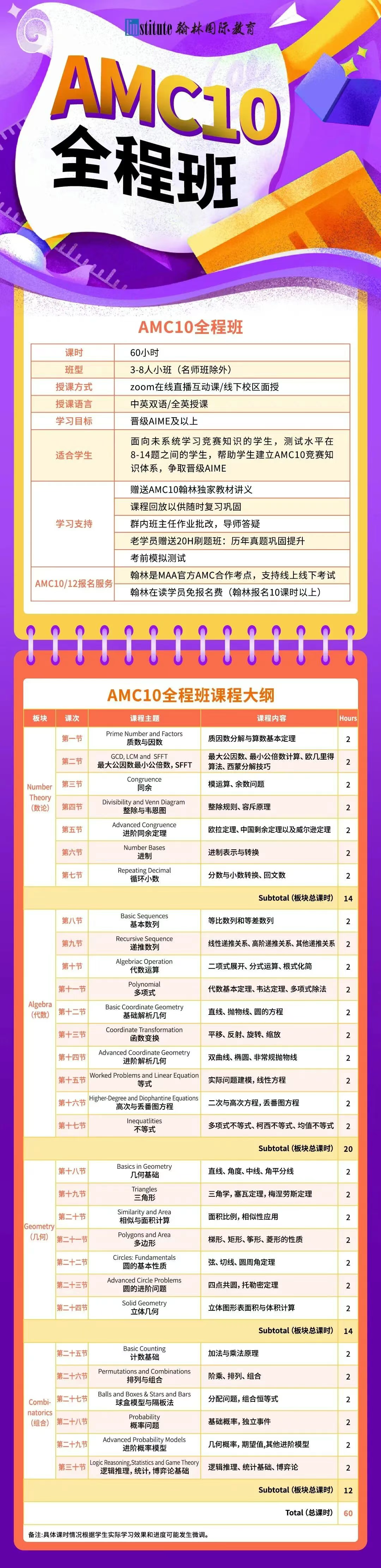
翰林AMC10培训班
翰林AMC10培训班