冲刺牛剑G5数学必备竞赛!
UKMT-SMC + UKMT-BMO 英国数学竞赛
新赛季报名火热进行中!
UKMT-SMC
🔹 报名截止:2025年10月2日
🔹 考试时间:2025年10月10日17:00-18:30
UKMT-BMO Round 1:
🔹 报名截止:2025年11月10日
🔹 考试时间:2025年11月19日17:00-20:30
UKMT-BMO Round 2:
🔹 报名截止:2026年1月12日
🔹 考试时间:2026年1月26日17:00-20:30
报名方式:
🔹 ASDAN合作学校报名:可以通过ASDAN报名;若自己学校是合作考点,可以在本校报名,通过校方统一组织。
🔹 翰林协助报名:若本校无法报名,可以由翰林协助学生报名。
UKMT英国大不列颠数学协会
UKMT(The United Kingdom Mathematics Trust英国大不列颠数学协会)是英国最大规模的数学竞赛,全球考生均可报名参加。UKMT为11-18岁的学生提供各种各样的国家级别的数学竞赛和数学活动,主要侧重于学生的数学能力和逻辑推理技巧。
UKMT作为通往国际数学奥林匹克竞赛(IMO)的重要桥梁,每年吸引全球约6000余所学校、70万名学生的热情参与,堪称英国规模最大、影响力最广泛的全国性数学竞赛盛事。

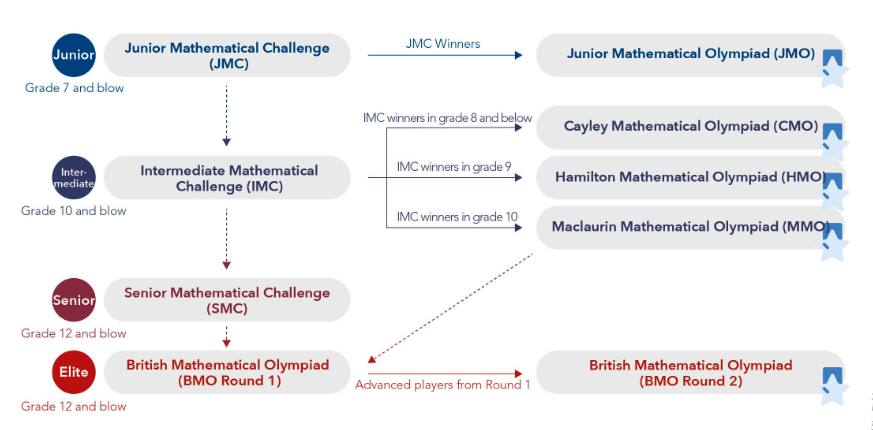
UKMT的数学竞赛体系,旨在全面检验学生的数学素养与逻辑推理能力,其竞赛项目依据难度梯度分为:
● 初级数学挑战赛 - 7年级及以下
(Junior Mathematical Challenge, JMC)
● 中级数学挑战赛 - 10年级及以下
(Intermediate Mathematical Challenge, IMC)
● 高级数学挑战赛 - 12年级及以下
(Senior Mathematical Challenge, SMC)
● 英国数学奥赛 - 高中任意年级
(British Mathematical Olympiad, BMO)
UKMT是用来选拔国际数学奥林匹克竞赛(IMO)选手的通道。
与IMO的晋级关系(英国):
SMC→BMO Round1→BMO Round 2→IMO
* 中国学生虽然可以直接报名参加BMO奥赛,但SMC的成绩依旧拥有很高的参考价值。
竞赛官网:https://ukmt.org.uk/
为什么SMC&BMO可以一起备考?
时间衔接紧密,形成备考链条
SMC在每年10月中旬举行,BMO Round 1在11月中下旬开赛,间隔约6周,可以形成“基础→高阶”的连贯路径。
学生可在SMC后立即进入BMO的深度训练,避免知识断层,高效利用备赛周期。
知识点高度重叠,BMO深化SMC基础
SMC与BMO均覆盖代数、几何、数论、组合数学四大领域,但考察深度不同;BMO的综合性应用题常融合多领域知识,而SMC可视为其简化版,为BMO的跨模块解题奠定思维基础。
竞赛机制关联,SMC作为BMO“热身赛”
在英国,SMC前10%(约1000人)可晋级BMO Round 1,中国学生虽可直接报名BMO,但SMC成绩仍具参考价值:
▪ SMC分数≥100分(满分125)相当于BMO入门水平,可预测备赛方向。
▪ SMC奖项(金奖前10%)可增强申请背景,与BMO奖项形成梯度证明。
SMC英国高级数学挑战赛
SMC(Senior Maths Competition),即英国高级数学测评比赛,由英国UKMT组织,面向12年级(高三年级)及以下的学生。
SMC的题目灵活、具有一定挑战性,考察学生使用数学能力解决实际问题的能力,是英国数学奥赛BMO的前置测评活动,具有较高的含金量和英本认可。
赛事形式
个人考试,线上作答,共90分钟,25道多项选择题。起始分数为25分,答对得4分,答错扣1分,不答得 0 分。
考察内容
通常涵盖几何(主要是平面几何),数论,排列组合,代数题和应用题,本考试不涉及高等数学知识。
数论
▪ Factor & Multiple 因数与倍数
▪ Prime Number 质数与合数
▪ Remainder 余数问题
▪ Complex Number Theory 复杂数论问题
代数
▪ Sequence 数列
▪ Polynomial 多项式
▪ Equation/Function/Graph 方程与函数
▪ Inequality 不等式
计数与概率
▪ Rule of Sum and Product 加乘原理
▪ Permutation & Combination 排列组合
▪ Inclusion-exclusion Principle 容斥原理
▪ Logic 逻辑分析
几何
▪ Triangle/Polygons 三角形和多边形
▪ Similar Triangle, Congruent Triangle 相似三角形,全等三角形
▪ Circle 圆
▪ Solid geometry 立体几何
奖项设置
英国排名前 66% 的选手将会按照 1:2:3的比例分别获得金奖、银奖和铜奖,中国学生将根据英国学生奖项分数线划定金、银、铜奖项。
⏩ 领取福利

真题预览(部分)
SMC历年真题
扫码领取!
BMO英国数学奥林匹克赛事
BMO英国数学奥林匹克竞赛是UKMT旗下针对高年级中学生的比赛项目。
赛事形式
考试以英文形式进行,每场考试3.5小时,每题10分,需要完全化简的答案以及完整的解答过程(部分过程正确也将获得一定的分数)。
Round 1需要完成6道简答题,Round 2需要完成4道简答题。
考察内容
通常涵盖几何学、三角学、函数方程、代数、数论、组合数学等。
数论
▪ 涉及到方程的整数解。
BMO1:
▪ 模10算术的规则及扩展内容。
BMO2:
▪ 了解费马小定理(Fermat's Little Theorem)等相关概念和定理。
代数
▪ 二次方程(quadratics)
▪ 因式定理(Factor Theorem)
BMO2:
▪ 柯西-施瓦茨不等式(Cauchy-Schwarz Inequality)
组合数学方面
BMO1:
▪ 二项式系数(Binomial Coefficients)
BMO2:
▪ 掌握鸽子洞原理(Pigeon-hole Principle)
▪ 掌握计数方法的建构过程的递归关系的概念会非常有帮助。
▪ 图论(Graph Theory)
几何
BMO1:
▪ 圆定律:交错弧定理(Alternate Segment Theorem)
BMO2:
▪ 基础的结构认知
▪ 三角形的4个中心点:外心、垂心、内心和重心
▪ 三角形面积计算的海伦公式(Heron's formula)
第一轮奖项设置
* 中国的参赛者将根据英国的截止分数进行评判
♚ 金奖 (Gold Medal): 授予英国排名前 20 的选手。
♚ 银奖 (Silver Medal): 授予英国排名 21-50 的选手。
♚ 铜奖 (Bronze Medal): 授予英国排名 51-100 的选手。
♚ 优秀奖 (Distinction): 授予约前 26% 的选手。
♚ 良好奖 (Merit): 授予约前 66% 的选手。
BMO第一轮晋级第二轮资格
BMO第二轮资格门槛:英国约前100名的学生可以晋级第二轮,中国学生会参照英国的分数线。
♚ 优秀奖 (Distinction): 授予前 25% 的选手。
♚ 良好奖 (Merit): 授予约前 48% 的选手。
⏩ 领取福利

真题预览(部分)
BMO历年真题
扫码领取!
为助力有志学子冲击英国数学SMC & BMO 奖项,翰林特设 SMC强化班、BMO强化班。课程由金牌导师领衔设计,聚焦核心考点与思维突破。
通过系统化知识梳理与高强度实战演练,直击竞赛难点,提升解题效率。翰林以科学的备考路径与全方位的资源支持,为学员铸就金奖竞争力!
英国数学思维挑战SMC课程大纲
1、Number Theory(数论)
◾Divisor Problems of integers
◾*Remainder Problems of integers
◾Digit Problems *in different base representations
◾Divisibility Problems
2、Algebra(代数)
◾Sequences
◾Algebraic Operations
◾Coodinate System and Functions
◾Solving Equations
◾Inequalities and Extreme Value Problems Triangles
3、Geometry(几何)
◾Triangles
◾Polygons
◾Circles
◾Simple Solid Geometry
4、Combinatorics(组合)
◾Counting Problems
◾Permutation Problems and Combination Problems
◾Simple Probability Problems
英国数学奥赛BMO课程大纲
1、Number Theory(数论)
专题:
◾Prime Factorization and All About Factors(质因数分解与整数的约数问题)
◾Euclidean Algorithm and Bezout's Theorem(欧几里得算法与裴蜀定理)
◾Congruence (同余理论)
◾Advanced Number Theory Results-Euler's Totient Theorem, Chinese Remainder Theorem, Wilson's Theorem(进阶数论相关结果:欧拉定理,中国剩余定理,威尔逊定理)
◾Method of Solving Diophantine Equaiton(丢番图方程的求解方法)
◾Base-n Representation and Base Converison(进位制表达与进位制转换)
2、Algebra(代数)
专题:
◾Recursive Sequences and Recursive Methods(递归数列与递归方法)
◾Polynomials(多项式理论)
◾Inequalities and Extreme Value Problems (基本不等式与极值问题)
◾Function Equations(函数方程)
◾Trigonometry(三角学)
3、Geometry(几何)
专题:
◾Basics in Geometry(几何基础)
◾Triangles(三角形及其相关性质)
◾Circles(圆及其相关性质)
4、Combinatorics(组合)
专题 :
◾Basic Counting Principles, Permutations and Combinations(基本计数原理,排列与组合)
◾Combinatorics Number and Combinatorics Indentities(组合数及组合恒等式)
◾Pigeon Holes Principle(鸽笼原理/抽屉原理)










