今天下午,2025年上海中考数学终于尘埃落定。上周的上海高考数学出乎意料的简单,那么这次中考难度到底如何呢?
某自媒体做了一个投票,结果呈现出两极分化的情况:

有说很简单,甚至班里几个同学对了一下都感觉不错;也有说比24年难,尤其是几道重点题。


简单和难,本来就因人而异,但既然出现两级分化,也说明这一次的中考题出得还是中规中矩的。
有趣的是,投票的有超过一半的是“吃瓜群众”,这其中应该不仅有26届或者其他年级的未来中考候选选手,也有很多关心中考的小学家长。虽然中考离自己的孩子还很远,甚至很多人连小升初这一关还没过,但中考无疑是一个风向标。
那么想要把初中数学学好能在中考中胜出,小学数学该打好哪些底子呢?小学参加各种数学竞赛,学了很多校外的内容,到了初中还有用吗?
可以说,付出一定有回报,但也有前提!
扫码添加顾问老师领取
《AMC 8预学全指导(Pre-AMC)》


更多信息可咨询顾问
小学竞赛的内容到初中就消失了?
“鸡兔同笼学了那么多方法有什么用?到了初中一个方程就搞定了”。这也许是很多家长的困惑。别说用方程就能解决小学里的大部分“难题”,甚至到了初中这样的文字应用题本身也少了很多。
那么是不是小学竞赛里的东西都“白学”了呢?当然不是。其实竞赛中的很多内容,是在给后续的学习做铺垫。
01从具象到抽象的铺垫
比如小学阶段有很多“巧算”题,无论凑整法、基准数法、重组法等,核心就是运算定律的灵活应用。小学阶段学的是“数”,到了初中阶段学的是“式”,虽然对象变了,但运算的规则没有变,并且在这个过程中还积累了“数感”(对数字关系的敏感直觉)。因此小学阶段如果能对运算定律的综合应用达到融会贯通,那么初中的代数式运算、因式分解等内容的学习会更加轻松。
同样,行程问题、等量代换等,虽然到了初中似乎都看不到了,但其实只是以动点问题、换元法等更抽象的形式出现了而已。
02从直觉猜想到逻辑论证的铺垫
尽管我们一直说“数学讲逻辑”,但其实整个小学阶段的学习,直觉的占比还是非常高的。举个例子:
在周长相等的情况下,探索不同长宽矩形的面积变化,小学的主要方式是“归纳推理”,比如利用下面的表,学生可以很直观地发现“长宽越接近、面积越大”。但这种结论并不严谨,到了初中学了二次函数后就能做非常严谨的“演绎推理”了。
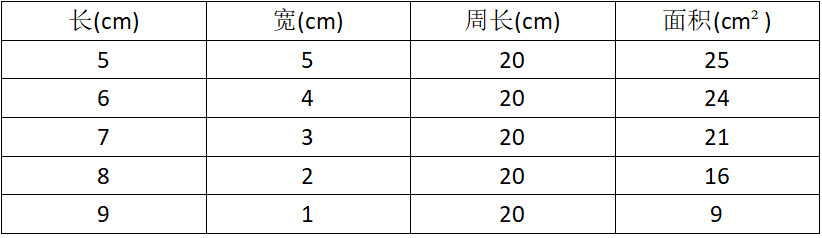
这也是为什么很多孩子到了初中学习会感到不适应的原因,因为初中无论是平面几何的证明还是代数式的推导,都要求更严谨的逻辑。
而在我们的竞赛思维课程中,其实有非常多的“好用”结论,这些结论怎么来的?一个好的老师应该会带孩子做比较细致的解释。比如数论中3的整除性,就需要通过位值原理来严格论证。

再比如斐波那契数列主题中的“爬楼梯”问题,既需要直觉感受数字规律,又需要利用递推的方式一步步发现规律背后的秘密。
因此,一个“不套路”的竞赛课程,是可以提前让学生了解到“正确做数学的方式”,并感受数学的逻辑美感的。
从这三个数学思想小学务必掌握
竞赛一般分为四大模块:数论、代数、几何、排列组合(国内小奥一般归为七大模块,但大同小异)。内容很多很杂,如果不是未来也走竞赛路线,必然有些东西会遗忘甚至以后完全不会碰,但也有一种东西是会贯穿小初高甚至其他学科学习的东西——数学思想方法。其中有三个在初中学习中最为常用:
01分类思想
分类思想可以说是整个数理思维的起点,并且贯穿了从幼儿园到大学的全部数学学习阶段。拥有分类思想的学生往往想问题“很全面”,并且能够“分而治之”。而在初中的数学学习中无孔不入,甚至开始逐渐成为拉开差距的重点,比如下面的一个简单问题却非常容易丢分:
设a、b、c是三个实数,请用a、b、c表示方程ax²+bx+c=0的解
很多同学直接就用一元二次方程的求根公式,但你是否忘了,题目并没有说这是二次方程啊,所以要分成a=0和a≠0进行讨论得到不同答案。这种错误看似是“粗心”,其实就是源于概念的细节没有把握好,以及没有分类讨论的意识。
分类思想在小学竞赛中非常常见,比如低年级熟悉的“数图形”问题,想要不漏不重复,最重要的就是要“先分类再数”。
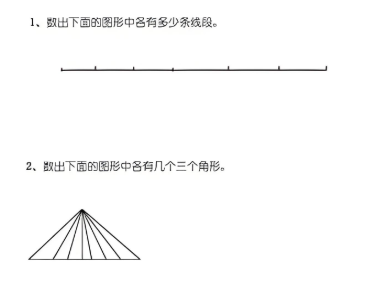
02数形结合思想
“数缺形时少直观、形缺数时难入微”,数形结合思想也几乎是可以渗透到每一个数学概念中的。尤其初中的很多概念越来越抽象,采用数形结合就能四两拨千斤,比如下面这个常见的绝对值化简问题,看上去是一道代数题,但利用“绝对值就是距离”这个直观解释,这题就变成了“a和b的距离是6、a和c的距离是10”,解起来就很方便了。
已知|a-b|=6,|a-c|=10,求|b-c|=______________
在竞赛思维课程中,数形结合思想几乎也是随时都会出现的,比如在解决“和差倍问题”时,利用线段图去理解题目;又或者在研究“乘法原理”时用树状图去整理不同分类情况。
03对应思想
其实从数数开始,就已经有了对应思想,而初中的一个重点“函数”,本质上就是对应思想的具体化和形象化。
利用对应思想有时候可以“降维打击”一些数学问题,比如下面这个问题:
有32个人参加乒乓球比赛,两两一组进行单打比赛,赢的人晋级下一轮,输的直接淘汰。请问一共需要多少比赛能产生冠军。
这个问题很多学生拿到就开始进行计算:32÷2=16、16÷2=8......
但其实这个题目只要用对应思想就可以秒解,因为“一场比赛淘汰一个人”,所以32个参赛者需要淘汰31个人,需要31场。
所以,学竞赛的孩子到了初中面对更抽象、更复杂的问题,可以说会更加游刃有余,因为即使没有超前学,内容可能陌生,但学习的方法反而会感觉很熟悉。
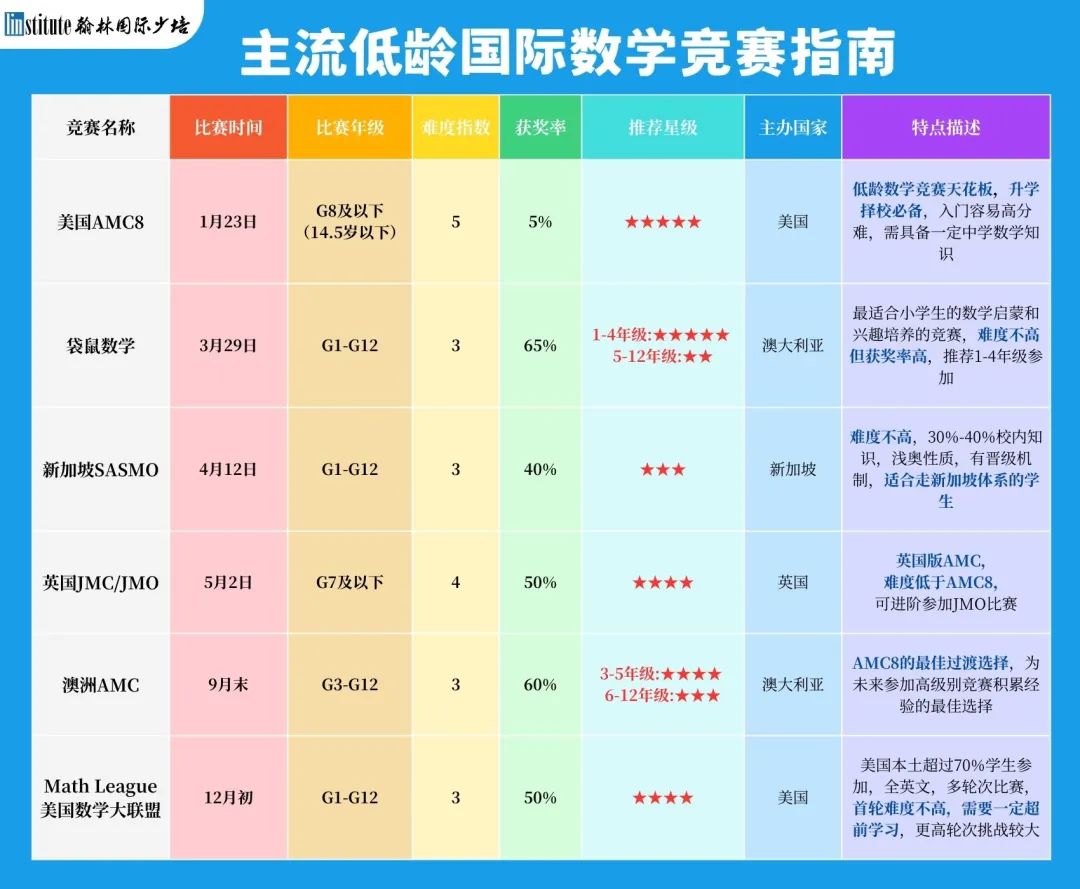
而竞赛带来的数学思维培养并非一朝一夕就能形成,好的老师和好的课程就非常关键啦。以下是主流低龄国际数学竞赛指南,同学们可以考虑参加哦👇。
了解更多请扫码添加顾问老师
同时可以领取:
《AMC 8预学全指导(Pre-AMC)》


更多信息可咨询顾问
翰林AMC8
全方位课程服务概览
⏬️⏬️⏬️

往期文章阅读推荐:










